What is Convolution?
4
SREV1 Sampling Guide
What is Convolution?
Convolution is a technique for imposing the characteristics of one signal onto another.
What the SREV1 does is to convolve the reverberation characteristics of a previously
sampled acoustic space (i.e., its impulse-response) onto another audio source, produc-
ing the same overall sound that would have been heard had the audio source actually
been heard in that acoustic space.
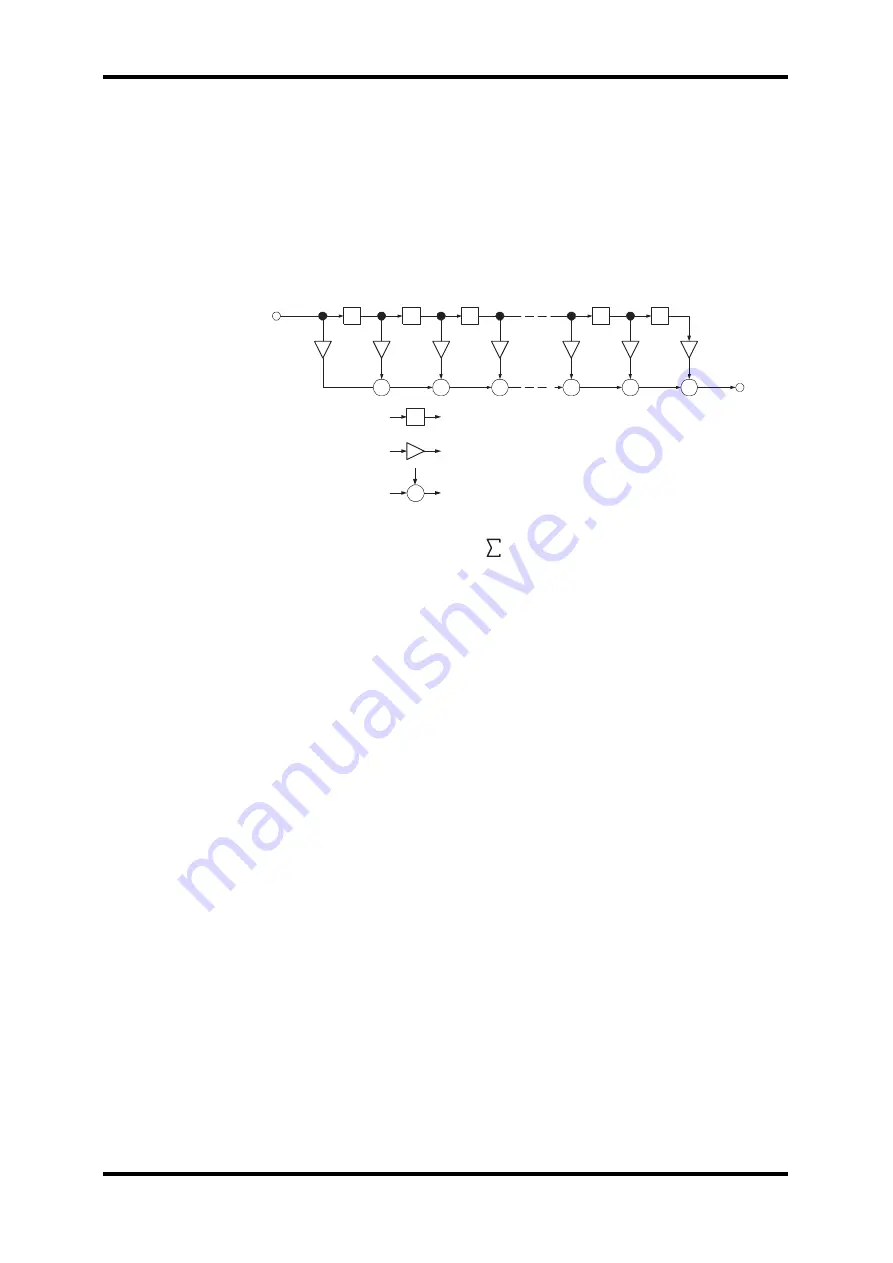
For the technically minded, the following diagram shows the signal flow and formula
for convolution processing.
What is an Impulse Response?
Just as a frequency response shows how an audio circuit responds to a range of frequen-
cies, an “impulse-response” shows how an acoustic space responds to an impulse signal.
And since the data acquired by measuring the impulse response of an acoustic space
consists not only of the original test signal, but acoustic information about that space
as well, we can use an impulse-response to measure reverberation.
No doubt you’ve clapped your hands in order to check the reverberation characteristics
of a hall. Well, since a hand clap is audibly similar to the sound of an impulse, this is
akin to hearing an impulse response. What you heard were the reverberation character-
istics of that acoustic space, your hands being the audio source, your ears the pickup
point. A handclap is nowhere near as accurate as an impulse signal, so it’s not strictly
the same as what we’re talking about here, but it’s close enough to give you some idea
of what we mean by an impulse response.
Generally speaking, “impulse response” is a response to a linear, time-invariant pulse.
“Linear” meaning undistorted, or in other words, the test signal does not affect the
reverberation characteristics. By “time-invariant” we mean that the reverberation char-
acteristics do not change over time. Conventionally, “time-invariant” is used to mean a
state that does not change, but here we are assuming that the reverberation character-
istics do not change from the time the test signal is output to the time sampling is com-
pleted.
Impulse signals are ideal for sound-field sampling because they have a very short play-
back time and a flat frequency response at all frequencies, subject to the limitations of
the recording and playback process.
D
D
+
D
+
+
x(n)
h(0)
h(1)
h(2)
h(3)
D
+
h(N-3)
D
+
h(N-2)
+
x(n)
x(n-1)
x(n-2)
x(n-3)
x(n-N+3)
x(n-N+2)
x(n-N+1)
h(N-1)
y(n)
D
+
: 1 sample delay
: multiplier
: adder
y(n) = h(i) * x(n-i)
N-1
i=0






































