LT8330
14
8330fa
For more information
www.linear.com/LT8330
also be wound on the same core, since identical voltages
are applied to L1 and L2 throughout the switching cycle.
For the SEPIC topology, the current through L1 is the
converter input current. Based on the fact that, ideally, the
output power is equal to the input power, the maximum
average inductor currents of L1 and L2 are:
I
L1(MAX)(AVE)
=
I
IN(MAX)(AVE)
=
I
O(MAX)
•
D
MAX
1
−
D
MAX
I
L2(MAX)(AVE)
=
I
O(MAX)
In a SEPIC converter, the switch current is equal to I
L1
+
I
L2
when the power switch is on, therefore, the maximum
average switch current is defined as:
I
SW(MAX)(AVE)
=
I
L1(MAX)(AVE)
+
I
L2(MAX)(AVE)
=
I
O(MAX)
•
1
1
−
D
MAX
and the peak switch current is:
I
SW(PEAK)
=
1
+
c
2
⎛
⎝
⎜
⎞
⎠
⎟
•
I
O(MAX)
•
1
1
−
D
MAX
The constant
c
in the preceding equations represents
the percentage peak-to-peak ripple current in the switch,
relative to I
SW(MAX)(AVE)
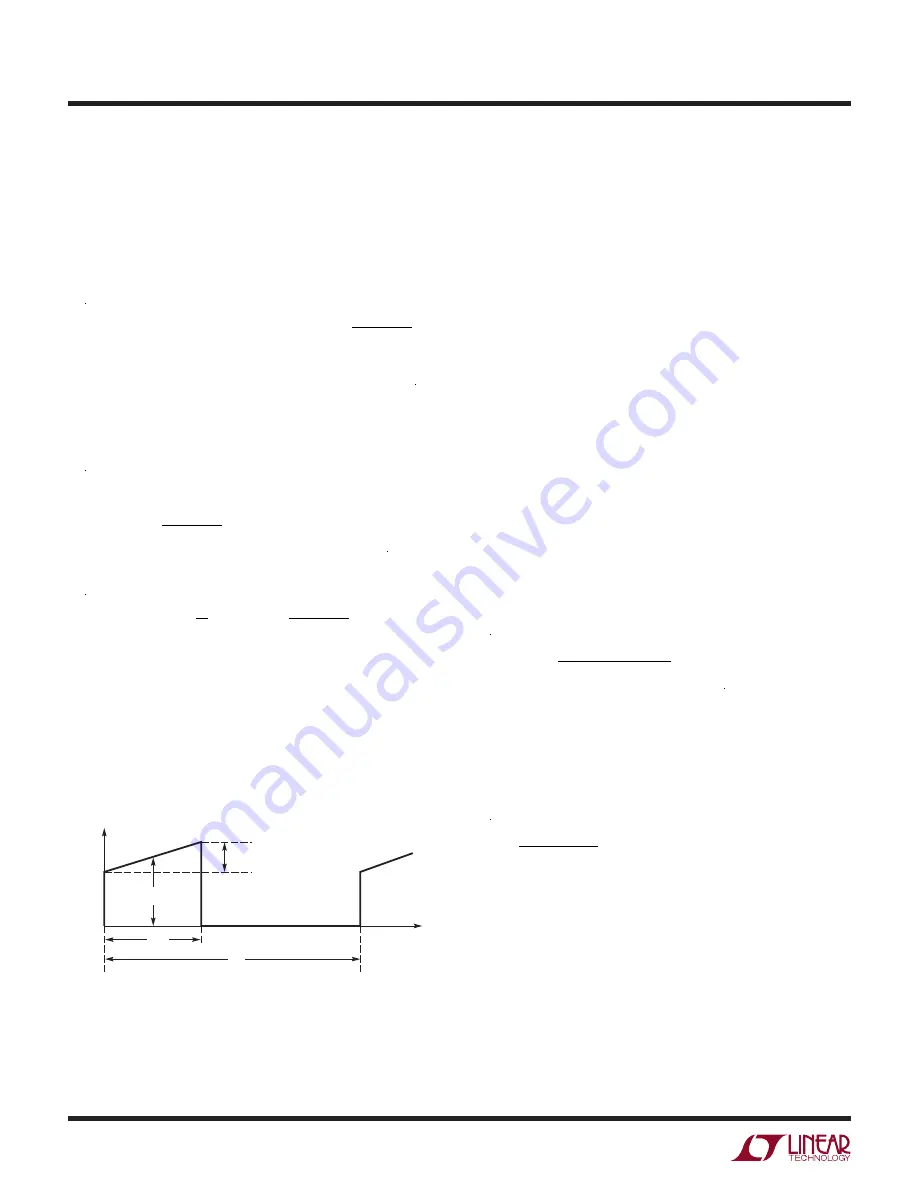
, as shown in Figure 6. Then, the
switch ripple current ∆I
SW
can be calculated by:
∆I
SW
=
c
•
I
SW(MAX)(AVE)
The inductor ripple currents ∆I
L1
and ∆I
L2
are identical:
∆I
L1
= ∆I
L2
= 0.5
•
∆I
SW
The inductor ripple current has a direct effect on the
choice of the inductor value. Choosing smaller values of
∆I
L
requires large inductances and reduces the current
loop gain (the converter will approach voltage mode).
Accepting larger values of ∆I
L
allows the use of low in-
ductances, but results in higher input current ripple and
greater core losses. It is recommended that
c
falls in the
range of 0.2 to 0.6.
Due to the current limit of its internal power switch, the
LT8330 should be used in a SEPIC converter whose
maximum output current (I
O(MAX)
) is less than the output
current capability by a sufficient margin (10% or higher
is recommended):
I
O(MAX)
< (1 – D
MAX
)
•
(1A – 0.5
•
∆
I
SW
)
•
(0.9)
Given an operating input voltage range, and having cho-
sen ripple current in the inductor, the inductor value (L1
and L2 are independent) of the SEPIC converter can be
determined using the following equation:
L1
=
L2
=
V
IN(MIN)
0.5
•
∆
I
SW
•
f
OSC
•
D
MAX
For most SEPIC applications, the equal inductor values
will fall in the range of 1µH to 47µH.
By making L1 = L2, and winding them on the same core, the
value of inductance in the preceding equation is replaced
by 2L, due to mutual inductance:
L
=
V
IN(MIN)
∆
I
SW
•
f
OSC
•
D
MAX
This maintains the same ripple current and energy storage
in the inductors. The peak inductor currents are:
I
L1(PEAK)
= I
L1(MAX)
+ 0.5
•
∆
I
L1
I
L2(PEAK)
= I
L2(MAX)
+ 0.5
•
∆
I
L2
The maximum RMS inductor currents are approximately
equal to the maximum average inductor currents.
applicaTions inForMaTion
Figure 6. The Switch Current Waveform of the SEPIC Converter
8330 F06
∆
I
SW =
χ
•
I
SW(MAX)(AVE)
I
SW
t
DT
S
I
SW(MAX)(AVE)
T
S










































