manualshive.com logo in svg

Cypress CapSense AN64846, Начало работы

Поделиться
Скачать
Cypress CapSense AN64846 Скачать руководство пользователя страница 16

   

CapSense Technology 

AN64846 - Getting Started with CapSense

®

 

Doc. No. 001-64846 Rev. *X 

16 

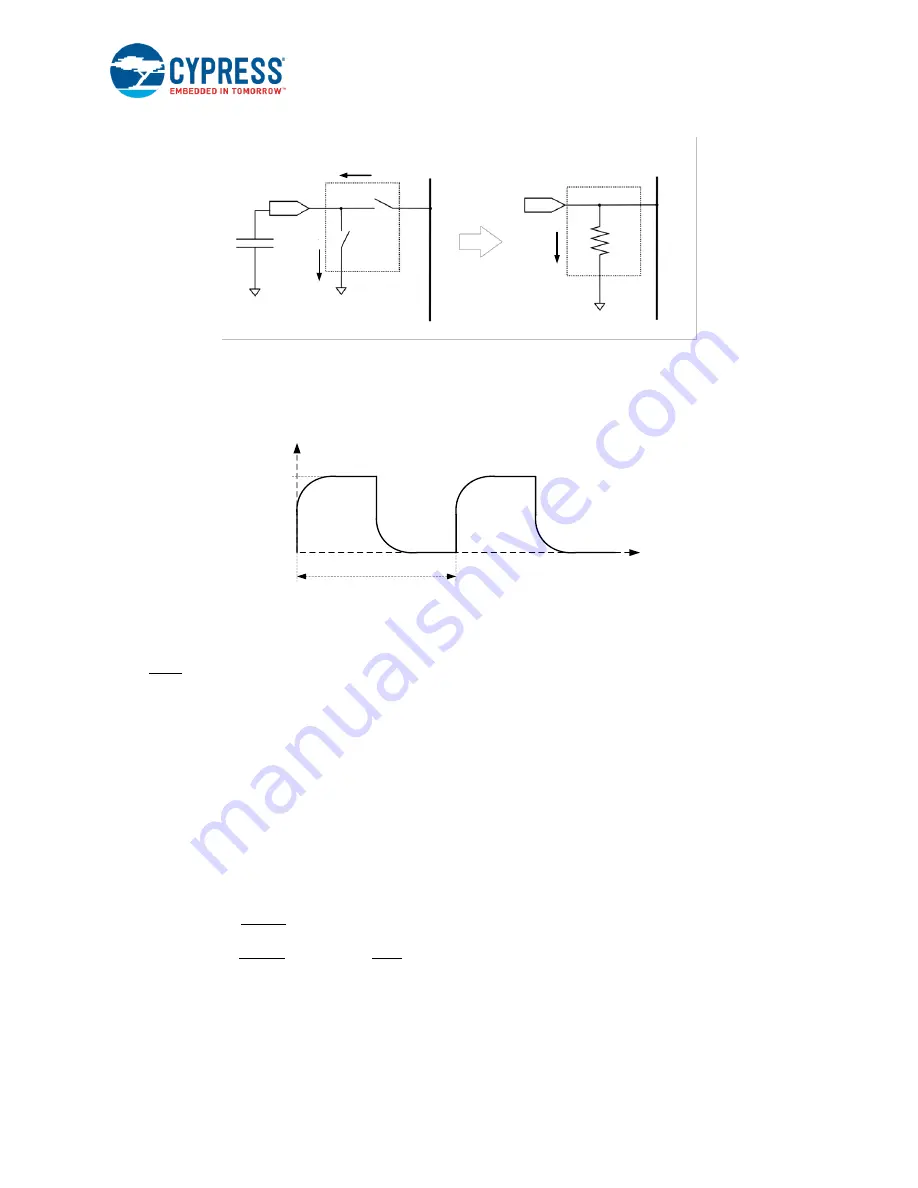
Figure 2-13. Equivalent Resistor Model 

C

S

R

eq

AMUXBUS

SW

1

SW

2

AMUXBUS

I

CS

I

CS

I

CS

 

Two non-overlapping, out-of-phase clocks of frequency F

SW

 (see 

Figure 2-14

) control the switches SW

1

 and SW

2

. F

SW

 

should be selected such that the sensor completely charges and discharges.  

Figure 2-14. Voltage Across Sensor Capacitance 

V

t

V

REF

(1.2V)

0

T

SW

 = 1/F

SW

SW

1

 OPEN

SW

2

 CLOSED

SW

1

 CLOSED

SW

2

 OPEN

 

 

The continuous switching of SW

1

 and SW

2

 forms an equivalent resistance R

eq

, as 

Figure 2-13 

shows. The value of the 

equivalent resistance R

S

 is: 

R

eq

=  

1

C

S

 F

SW

 

 

Equation 3 

Where: 

C

S

 = Total sensor capacitance = Parasitic capacitance (C

P

) + Finger capacitance (C

F

) 

F

SW

 = Frequency of the switching clock or Sense Clock Frequency 

Equation 4 gives the average current taken by the sensor capacitor from the AMUXBUS.  

I

CS

  = C

S

 F

SW

V

REF

 

Equation 4 

Equation 5  shows  the  raw  count  equation  when  only  Modulation  IDAC (single  IDAC mode)  is  used  and  Equation  6 
shows the raw count when both Modulation IDAC and Compensation IDAC (Dual IDAC mode) are used. The dual IDAC 
mode gives more sensitivity and produces more count for a specific finger capacitance compared to the single IDAC 
mode.  

R

aw count = (2

N

− 1)

 V

REF

 F

SW

I

MOD

 C

S

  

Equation 5 

Raw count = (2

N

− 1)

 V

REF

 F

SW

I

MOD

 C

S

− (2

N

− 1)

 I

COMP

I

MOD

         

 

Equation 6  

Where:  

N = Scan resolution of the Sigma-Delta modulator in bits. CSD supports up to 16-bit resolution.  

The CapSense architecture and its features vary slightly depending on the device. For example, some devices do not 
support dual IDAC mode. The architecture presented here is available in many of the CapSense controllers. Refer to 
the device-specific 

Design Guide

 to learn about the sensing technology implemented for that device.  

Содержание CapSense AN64846

Страница 1: ...AN64846 Getting Started with CapSense Document No 001 64846 Rev X Cypress Semiconductor 198 Champion Court San Jose CA 95134 1709 http www cypress com ...

Страница 2: ...rising out of any security breach such as unauthorized access to or use of a Cypress product In addition the products described in these materials may contain design defects or errors known as errata which may cause the product to deviate from published specifications To the extent permitted by applicable law Cypress reserves the right to make changes to this document without further notice Cypres...

Страница 3: ...nse Auto Tuning 19 2 5 Signal to Noise Ratio SNR 21 2 5 1 Measuring SNR 22 2 6 CapSense Widgets 22 2 6 1 Buttons Zero Dimensional Sensors 23 2 6 2 Sliders One Dimensional Sensors 24 2 6 3 Touchscreens and Trackpads Two Dimensional Sensors 26 2 6 4 Proximity Three Dimensional Sensors 26 2 7 Sensor Construction 27 2 7 1 Field Coupled Via Copper Trace PCB 27 2 7 2 Field Coupled Via Spring Gasket Foam...

Страница 4: ...3 Median Filter 57 3 4 4 Jitter Filter 58 3 4 5 Event Based Filters 60 3 4 6 Rule Based Filters 60 3 5 Power Consumption 60 3 5 1 Active and Sleep Current 60 3 5 2 Average Current 60 3 5 3 Response Time Versus Power Consumption 61 3 6 Proximity Sensing Design 62 3 6 1 Implementing Proximity Sensing with CapSense 62 3 6 2 Proximity Sensor Design 64 3 6 3 Factors Affecting Proximity Distance 65 3 7 ...

Страница 5: ...ools 106 5 3 3 CapSense Tuner 106 5 3 4 EZ Click 107 5 3 5 Bridge Control Panel 107 5 4 Development Kits 107 5 4 1 PSoC 4 Development Kits 107 5 4 2 PSoC 3 and PSoC 5LP Development Kits 107 5 4 3 CapSense Express Development Kits 108 5 4 4 PSoC 1 Development Kits 108 5 4 5 Kits for Programming and Debugging 108 5 5 Design Support 108 A Springs 109 A 1 Finger Introduced Capacitance 109 A 1 1 Mounti...

Страница 6: ...s 118 B 2 6 Ground Plane Mesh 118 B 2 7 Series Resistor 118 B 2 8 Shield Electrode 119 B 2 9 Guard Sensor 119 C Clearance Between Sensor and Ground 120 D PSoC 1 In Circuit Emulation ICE Pods 123 D 1 Evaluation Pods 123 D 2 In Circuit Emulation ICE Pod Kits 123 Glossary 124 Revision History 129 ...

Страница 7: ...based design Mechanical buttons are less reliable and wear out over time due to the physical movement CapSense designs do not involve moving parts Mechanical buttons pose problems when moisture seeps through the gaps in the assembly CapSense based front panels can be completely sealed under the overlay Mechanical buttons require a small force to operate compared to the touch buttons and this force...

Страница 8: ...required for CapSense operation These parameters vary depending on the board layout sensor dimensions overlay properties and application requirements such as power consumption and response time Therefore this step is usually performed when the pre production builds are available Many of the CapSense devices support Cypress s Auto tuning algorithm called SmartSense that automatically sets parameter...

Страница 9: ...nd source code C cd icc Italics Displays file names and reference documentation Read about the sourcefile hex file in the PSoC Designer User Guide File Open Represents menu paths File Open New Project Bold Displays commands menu paths and icon names in procedures Click the File icon and then click Open Times New Roman Displays an equation 2 2 4 Text in gray boxes Describes Cautions or unique funct...

Страница 10: ... firmware See the Glossary for the definitions of CapSense terms Figure 2 1 Illustration of a Capacitive Sensor Application 2 1 CapSense System Overview CapSense touch sensing solutions include the entire system environment in which they operate This includes Hardware components such as PCB and guard sensor Firmware component to process the sensor data 2 1 1 Hardware Component The CapSense control...

Страница 11: ...CapSense system performance Best practices are discussed in the device specific Design Guides Figure 2 3 Two Layer Stack Up of a CapSense Board 2 1 1 1 Ground Plane In general a proper ground plane on the PCB reduces both RF emissions and interference However solid grounds near CapSense sensors or traces connecting these sensors to the PSoC pins increase the parasitic capacitance of the sensors Th...

Страница 12: ...modate firmware development in C and assembly languages See Software Tools for more information on this and other tools 2 2 Capacitive Sensing Methods Capacitance can be measured between two points using either self capacitance or mutual capacitance The left side of Figure 2 6 shows the self capacitance method and the right side shows the mutual capacitance method Figure 2 6 Self Capacitance and M...

Страница 13: ...hen a finger touches the sensor surface it forms a simple parallel plate capacitor with the sensor pad through the overlay The result is called finger capacitance CF and is defined by Equation 1 CF is a simplification of a distributed capacitance that includes the effects of the human body and the return path to the circuit board ground 𝐶𝐹 𝜀0𝜀𝑟 𝐴 𝐷 Equation 1 Where ε0 Free space permittivity εr Di...

Страница 14: ...ced between the TX and RX electrodes the mutual capacitance decreases to C1 M as shown in Figure 2 10 Because of the reduction in mutual capacitance the charge received on the RX electrode also decreases The CapSense system measures the amount of charge received on the RX electrode to detect the touch no touch condition Figure 2 9 Mutual Capacitance Sensing Working Overlay RX TX TX RX Electrode PC...

Страница 15: ...CapSense with Sigma Delta Modulator CSD Cypress s CSD method shown in Figure 2 12 uses a switched capacitor circuit on the front end of the system to convert the sensor capacitance CP to an equivalent resistor see Figure 2 13 A Sigma Delta modulator then converts the current measured through the equivalent resistor into a digital count When a finger CF is on the sensor the capacitance increases an...

Страница 16: ...cy Equation 4 gives the average current taken by the sensor capacitor from the AMUXBUS ICS CS FSWVREF Equation 4 Equation 5 shows the raw count equation when only Modulation IDAC single IDAC mode is used and Equation 6 shows the raw count when both Modulation IDAC and Compensation IDAC Dual IDAC mode are used The dual IDAC mode gives more sensitivity and produces more count for a specific finger c...

Страница 17: ... detailed explanation of the CapSense hardware in PSoC 4 S Series PSoC 4100S Plus and PSoC 4100PS devices Refer to PSoC 4100S and PSoC 4100S Plus PSoC 4 Architecture Technical Reference Manual TRM PSoC 4000S Family PSoC 4 Registers Technical Reference Manual TRM and PSoC 4100S Plus Registers Technical Reference Manual TRM for the basic knowledge of fourth generation CapSense architecture 2 4 CapSe...

Страница 18: ...e raw count signal raw count baseline sensor OFF sensor OFF sensor ON Difference Count or Signal Subtracting the baseline level from the raw count produces the difference count that is used in the ON OFF decision process The thresholds are offset by a constant amount from the baseline level The thresholds have the following functions Noise Threshold A parameter used to differentiate signal from no...

Страница 19: ...CapSense sensor automatically at power up and then monitors and maintains optimum sensor performance during runtime The number of parameters to be tuned is reduced from 17 in CSD to 4 with SmartSense Power up tuning SmartSense tunes the parameters of each sensor based on the individual sensor parasitic capacitance to get the desired sensitivity for the sensor Runtime tuning Noise in the system is ...

Страница 20: ...matically allowing seamless transition from one model to another with minimal or no tuning required Figure 2 17 Different Noise Levels in Design A and B Being Compensated Automatically 2 4 2 3 2 Noise Spikes During Production SmartSense technology also automatically tunes out the noise spikes in production that may not be seen during the design stage as indicated in Figure 2 18 This is a powerful ...

Страница 21: ... For CapSense applications signal is defined as the change in the raw count between the OFF and ON states Signal is also called Difference Count Noise is another term that has many meanings The following discussion presents a definition of CapSense noise that uses a simple mathematical model of the sensor output over time When the sensor is in the OFF state the counts X t can be modeled by an aver...

Страница 22: ...filling the bucket and nonlinear threshold events Another factor to consider is how the signal is produced The worst case ON and OFF scenario should be used when measuring SNR If the system is designed to sense the presence of a finger then measure SNR with a light touch of the sensor area and position the contact point slightly off center For automated testing a worst case finger touch 0 1 pF can...

Страница 23: ...ounded copper hatch separated by an annular gap Each button requires one I O pin of the CapSense controller Figure 2 21 Typical Simple Buttons 2 6 1 2 Matrix Buttons In applications requiring a high number of buttons such as a calculator keypad or a QWERTY keyboard capacitive sensors can be arranged in a matrix as Figure 2 22 shows This allows a design to have more buttons than there are I O pins ...

Страница 24: ...cation a slider with five segments can resolve at least 100 physical finger positions on the slider High resolution makes for smooth transitions in light or sound as a finger glides across a slider 2 6 2 1 Linear Sliders In a linear slider each CapSense controller I O pin is connected to one slider segment A zigzag pattern double chevron as shown in Figure 2 23 is recommended for slider segments T...

Страница 25: ...O pin is connected to two different slider segments This allows a design to have twice as many slider segments as there are I O pins For example a diplexed 16 segment slider requires only eight CapSense controller I O pins Figure 2 25 16 Segment Diplexed Slider For a diplexed slider to work properly the slider segments must be connected to the CapSense controller I O pins in a pre determined order...

Страница 26: ...enabling it to locate a finger s position in both X and Y dimensions Figure 2 27 shows a typical arrangement of a track pad sensor Figure 2 27 Trackpad Sensor Arrangement 2 6 4 Proximity Three Dimensional Sensors Proximity sensors detect the presence of a hand or other conductive object before it makes contact with the touch surface Imagine a hand stretched out to operate a car audio system in the...

Страница 27: ...each method so that you can choose one that fits your requirements 2 7 1 Field Coupled Via Copper Trace PCB Figure 2 29 Field Coupled Using PCB Features of a PCB based design Most common implementation Copper pads etched on the surface of the PCB act as sensor pads Electric field emanates from the copper sensor pad to ground plane No mechanical moving parts A nonconductive overlay serves as the to...

Страница 28: ...ectric field coupled with printed or deposited patterns on glass Higher series resistance of ITO films compared to copper No mechanical moving parts Ideal topology for graphical front panels 2 8 Liquid Tolerance CapSense is used in a variety of applications such as home appliances automotive and industrial applications These applications require robust CapSense operation even in the presence of mi...

Страница 29: ... a hatch fill connected to ground improves the noise immunity of the sensor The parasitic capacitance of sensor is denoted as CS in Figure 2 33 b Figure 2 33 Typical CapSense System Layout BTN1 Hatch Fill Connected to Ground Button Sensor 560 Ω CapSense Controller CapSense Controller 560 Ω CS a b As shown in Figure 2 34 when a liquid droplet falls on the touch surface due to its conductive nature ...

Страница 30: ...droplet is kept at the same potential the capacitance CLD added by the liquid droplet is nullified Because the voltage difference across the capacitance CLD is zero it will not draw any charge from the AMUX bus and therefore the increase in the raw count when a liquid droplet falls on the sensor will be very small as Figure 2 37 shows Figure 2 36 Capacitance Added by Liquid Droplet when the Hatch ...

Страница 31: ...e the best liquid tolerance performance it is required that the driven shield signal has the same voltage and phase as that of the sensor switching signal Figure 2 38 Driven Shield Signal Buffer Sensor Switching Signal Driven Shield Signal In Phase Sensor and Shield Signal 2 8 3 Guard Sensor When a continuous liquid stream is applied to the touch interface the liquid stream adds a large capacitanc...

Страница 32: ... the sensor In applications such as an induction cook top there might be chances of hot water spilling on the CapSense touch surface To determine the impact of temperature of a liquid droplet on the liquid tolerance performance tests were done with liquid droplets at different temperatures Experiment results show that the effect of hot liquid droplets is the same as that of the liquid droplets at ...

Страница 33: ... as explained below Face detection in mobile phones and tablets Face detection is a feature in mobile phones that disables the phone s touchscreen and dims the brightness of the display when a user answers a phone call as Figure 2 41 shows Face detection prevents false touches when the phone is placed on the ear and optimizes the device s power consumption Using proximity sensing based on CapSense...

Страница 34: ...an movement of the onscreen map Figure 2 44 Gesture Detection Implementation in a Laptop IR replacement Proximity sensors based on CapSense can replace IR proximity sensors in applications such as faucets and soap dispensers as Figure 2 45 shows Proximity sensing based on CapSense offers the following advantages over IR proximity sensing It is a low cost solution compared to IR proximity sensing P...

Страница 35: ...esign multiple types of feedback can be used in combination 2 10 1 Visual Feedback LEDs and LCDs provide visual feedback 2 10 1 1 LED Based Visual Feedback Visual feedback is widely used in user interfaces LEDs are used to indicate the status of buttons sliders and proximity sensors LEDs can implement different effects when the sensor status changes as listed below LED ON OFF GPOs are used to driv...

Страница 36: ...ure 2 46 Hitachi Dot Matrix LCD Pin Connections Character LCD with I2 C Interface PSoC can also control LCDs through I2 C with support for the NXP PCF2119x command format Figure 2 47 shows the typical circuit diagram for driving an LCD with I2 C interface Refer to the component datasheet to learn more Figure 2 47 Interfacing an LCD with I2C Interface PSoC LCD Module VDD SCL SDA Segment LCD Glass P...

Страница 37: ...espond fast making them suitable for typing applications but they cost more than ERM and LRA actuators Though their instantaneous current draw is more at around 300 mA at 3 V supply their average current consumption is not more than the ERM and LRA actuators Electro Active Polymer Actuators EAPs EAPs offer a performance similar to that of the piezo modules but integrating them into tight spaces is...

Страница 38: ...CapSense Technology AN64846 Getting Started with CapSense Doc No 001 64846 Rev X 38 Figure 2 49 Implementing Audible Feedback for CapSense ...

Страница 39: ...he geometry of a CapSense system is more complex than a parallel plate capacitor The conductors in the sensor include the finger and PCB copper However like a parallel plate capacitor CF is directly proportional to εr High dielectric constants lead to high sensitivity Because air has the lowest dielectric constant any air gaps between the sensor pad and overlay must be eliminated Dielectric consta...

Страница 40: ...he sensitivity of the system by eliminating any air gaps between overlay and the sensor pads 3M makes a high performance acrylic adhesive called 200MP that is widely used in CapSense applications in the form of adhesive transfer tape product numbers 467MP and 468MP 3 2 ESD Protection Robust ESD tolerance is a natural byproduct of a thoughtful system design By considering how contact discharge will...

Страница 41: ...withstand 12 kV Figure 3 2 ESD Path Air Filled Space PCB CapSense Non Conductive Material ESD Event Mechanical Structure Exposed Mounting Hardware ESD Event L2 L1 If it is not possible to maintain adequate distance place a protective layer of a high breakdown voltage material between the ESD source and CapSense controller One layer of 5 mil thick Kapton tape will withstand 18 kV See Table 3 3 for ...

Страница 42: ...C Considerations EMC is related to the generation transmission and reception of electromagnetic energy that can upset the working of an electronic system The source emitter produces the emission and a transfer or coupling path transfers the emission energy to a receptor where it is processed resulting in either desired or undesired behavior Electronic devices are required to comply with specific l...

Страница 43: ...e and emission Figure 3 5 RC Filter CapSense Controller CapSense Sensor External Series Resistor Pins Capacitance Series resistors should be placed close to the PSoC pins so that the radiated noise picked by the traces gets filtered at the input of the PSoC device Thus it is recommended that you place series resistors within 10 mm of the PSoC pins 3 3 1 1 2 1 CapSense Input Lines The sensor must b...

Страница 44: ...ired performance The rule of thumb is to allow a period of 5RSCS for charging and discharging cycles Equations for the minimum time period and maximum frequency are TSW minimum 10RSCS FSW maximum 1 10RSCS 3 3 1 1 2 2 Digital Communication Lines Communication lines such as I2 C and SPI also benefit from series resistance and 330 Ω is recommended for communication lines Communication lines have long...

Страница 45: ... keeping the power and signal loop areas as small as possible Stitch all the grounds with as many vias as possible This will reduce the overall ground impedance High frequency traces such as those used for clock and oscillator circuits should be contained by two ground lines This will ensure that there is no coupling which results in crosstalk Use separate ground plane and power planes wherever po...

Страница 46: ...reduced by connecting the two grounded areas Figure 3 10 Proper Current Loop Layout CapSense Sensor CapSense mC Ground Fill Connected Path to Sensor Pad Return Path PCB Other Circuitry 3 3 1 1 5 Frequency Hopping Frequency hopping is a method of spreading the input or operating frequency over a narrow band of frequencies This method helps to reduce the peaks and spread out the emissions as well as...

Страница 47: ...t P1 4 to be used to supply the external clock In this case pin P1 4 drive mode must be set to HI Z digital This increases the immunity to RF interference and spreads the emissions Pseudo random sequencer PRS A PRS is used instead of a fixed clock source to attenuate the emitted noise on CapSense pins by reducing the amount of EMI created by a fixed frequency source and to increase the EMI immunit...

Страница 48: ... the immunity against RF interference Figure 3 13 Immunity Level Selection 3 3 1 3 Radiated Emissions 3 3 1 3 1 Operating Voltage For devices in which sensors switch between an operating voltage and a reference voltage such as CY8C21x34 reducing the operating voltage helps to reduce emissions to a great extent This is because the amplitude of the switching signal at any pin is dependent on the dev...

Страница 49: ...can take more time to scan the sensors and perform the processing Therefore lower the system frequency depending on your application 3 3 1 3 3 Sensor Switching Frequency The CapSense sensing methods use a switched capacitor front end to interact with sensors Selecting a low frequency for the switched capacitor clock helps you to reduce the radiated emissions from the CapSense sensors Figure 3 15 s...

Страница 50: ...missions T tON A Amplitude Frequency AtON T 0 dB decade 20 dB decade 1 πtON tON tr tf A A 2 T Amplitude Frequency AtON T 0 dB decade 20 dB decade 1 πtON 1 πtr 40 dB decade 0 3 3 1 3 5 Sensor Scan time The scan time of sensors impacts radiated emissions Figure 3 17 shows the impact of the sensor scan time on radiated emissions An increase in the sensor scan time results in increased emissions Table...

Страница 51: ...sensors for liquid tolerance and for proximity sensing See the Shield Electrode and Guard Sensor section for more details The shield signal is a replica of the sensor signal The shield signal further increases radiated emissions as it is a high frequency switching signal and is driven on a spread out hatch fill Figure 3 18 shows the emissions with and without the driven shield signal Figure 3 18 I...

Страница 52: ...e 3 19 Drive Mode Selection for Shield Add a passive low pass filter LPF to the shield signal by putting a series resistor to the shield pin An inherent LPF is formed by the resistance of the electrode material and the parasitic capacitance of the electrode Therefore adding a series resistor increases the RC of the filter and helps to improve emissions to a great extent because the RC filter forme...

Страница 53: ...m Thus it improves the conducted noise immunity of the system A pi filter is a simple bidirectional low pass filter The two main types of pi filters are the series inductor and the series resistor The series inductor pi filter has two shunt capacitors and one series inductor configured similar to the Greek letter π as shown in Figure 3 21 The noise is filtered by all three elements L1 C1 and C2 in...

Страница 54: ...ensor data Commonly used to block generation or posting of nonexistent events Rule Based Nonlinear filter that causes a predefined response to a pattern observed in the sensor data Commonly used during normal operation of the touch surface to respond to special scenarios such as accidental multi button selection 3 4 1 Average Filter An average filter is a finite impulse response FIR filter with eq...

Страница 55: ...tered Figure 3 24 Average Filter Finger Touch 16 Samples The previous examples are representative of power supply noise The filter works well in this example because the period of the noise is close to the length of the filter N 16 For more information about how to implement an average filter see the code example CSA Software Filters with EzI2Cs Slave on CY8C20XX6 ...

Страница 56: ...uency noise components and pass lower frequency signals such as finger touch response waveforms Figure 3 25 IIR Filter Step Response The general equation for a first order IIR filter is 𝑦 𝑖 1 𝑘 𝑥 𝑖 𝑘 1 𝑦 𝑖 1 Equation 17 Figure 3 26 and Figure 3 27 illustrate the results of a first order IIR filter on real CapSense data using the filter equation with k 16 𝑦 𝑖 1 16 𝑥 𝑖 15 𝑦 𝑖 1 Equation 18 Figure 3 ...

Страница 57: ... filter a buffer of size N stores the N most recent samples of the input The median is then computed using a two step process First the buffer values are sorted from smallest to largest then the middle value is selected from the ordered list The buffer is scanned for the median with each update of the buffer This is a nonlinear filter The general equation for a median filter is 𝑦 𝑖 𝑚𝑒𝑑𝑖𝑎𝑛 𝑥 𝑖 𝑥 𝑖 ...

Страница 58: ...y on the slider the estimate of finger position will appear to shake and jitter even when the finger is held at a fixed position This jitter noise can be removed using a jitter filter To do this the previous input is stored in a buffer The current input is compared to the previous output If the difference is greater than 1 the output is changed by 1 matching sign as shown in Equation 21 This is a ...

Страница 59: ...put changes by less than the threshold amount The general equation for a jitter filter applied to buttons is 𝑦 𝑖 𝑥 𝑖 𝑡ℎ𝑟𝑒𝑠ℎ𝑜𝑙𝑑 𝑖𝑓 𝑥 𝑖 𝑦 𝑖 1 𝑡ℎ𝑟𝑒𝑠ℎ𝑜𝑙𝑑 Equation 22 𝑦 𝑖 𝑥 𝑖 𝑡ℎ𝑟𝑒𝑠ℎ𝑜𝑙𝑑 𝑖𝑓 𝑥 𝑖 𝑦 𝑖 1 𝑡ℎ𝑟𝑒𝑠ℎ𝑜𝑙𝑑 𝑦 𝑖 𝑦 𝑖 1 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 Figure 3 31 and Figure 3 32 show the result of using a jitter filter on real button data with a large component of periodic noise Figure 3 31 Jitter Filter for Button Noise Figu...

Страница 60: ...ed For example with a set of radio channel selection buttons two buttons can be touched accidentally but only one should be selected The rule based filter sorts out these kind of situations in a predefined way Another example is having a virtual sensor in CapSense applications The virtual sensor is not expected to be triggered during normal operation of the sensors but it may occur in unexpected s...

Страница 61: ...or response time of the CapSense button Because of this tradeoff between response time and power consumption the application developer must carefully select the sleep time based on system requirements In any application if both power consumption and response time are important parameters to be considered then an optimized method can be used that incorporates both continuous scan and sleep scan mod...

Страница 62: ...ensor layout guidelines such as proximity sensor type and size refer to the section Proximity Sensor Design and Factors Affecting Proximity Distance 6 Build the prototype After the schematic and layout design is completed build the prototype of the design to check if the design meets the performance requirements 7 Tune Tune the prototype board to achieve the required performance See the AN92239 Pr...

Страница 63: ...imity Sensing Specify Proximity Sensing Requirements Study Feasibility and Select Part Design CapSense Schematic Layout and Mechanical Structure Proximity Performance is Satisfactory Build Prototype Tune the Prototype Mass Production End Tune the Prototype Proximity Performance is Satisfactory Increase Sensor Size or Reduce Noise in the System Revisit Proximity Requirements Yes No Yes No 1 2 3 4 5...

Страница 64: ...that the CP of the ganged sensor does not cross the maximum CP limit of 45 pF Refer to AN92239 for details on how to implement proximity sensing using sensor ganging Figure 3 36 CapSense based Proximity Sensing with Sensor Ganging Button Sensor CapSense Circuitry Button Sensor Button Sensor AMUXBUS Multiple sensors connected to CapSense circuitry Button Sensor CapSense Circuitry Button Sensor Butt...

Страница 65: ...portional to the area of the sensor A proximity sensor implemented with the button sensor typical diameter of 5 15 mm has a small proximity sensing distance compared to a proximity sensor implemented using a PCB trace or wire with a diameter of 1 30 cm Therefore the required proximity sensing distance decides the selection of the proximity sensor type Table 3 7 shows when to use a specific proximi...

Страница 66: ...nship between the sensor size and the proximity sensing distance Depending on the end system environment the proximity sensing distance may vary for a specific sensor size You can find the sensor size needed to achieve a required proximity sensing distance by making sensor prototypes You can use a copper foil as Figure 3 39 shows to make a quick sensor prototype to determine the sensor size needed...

Страница 67: ...ottom layer of the PCB if there is any with the driven shield signal A hatch fill that is connected to the driven shield signal is called a shield electrode The driven shield signal is a replica of the sensor signal For shield electrode layout guidelines see Shield Electrode and Guard Sensor To minimize the sensor trace length and thereby the sensor CP place the CapSense device as close as possibl...

Страница 68: ...ensing distance Firmware filters help in reducing the noise thereby increasing the SNR and the proximity sensing distance You can use IIR median average or ALP filters to reduce the noise Refer to the Software Filtering section for details on IIR median and average filters Refer to the application note AN92239 for details on the ALP filter 3 6 3 3 System Parameters Power consumption Proximity sens...

Страница 69: ...duce the proximity distance by a drastic amount unlike a large grounded floating conductive object 3 7 Pin Assignments An effective method to reduce interaction between CapSense sensor traces and communication and non CapSense traces is to isolate each by port assignment Figure 3 44 shows a basic version of this isolation for a 32 pin QFN package Because each function is isolated the CapSense cont...

Страница 70: ...is is an example of a bad pin assignment Figure 3 45 Not Recommended CapSense and Non CapSense Pins in Proximity CapSense Controller VDD VDD PWM or other Non CapSense traces Communication traces X X The example in Figure 3 46 achieves good isolation but it has a bad pin assignment because the LEDs are placed next to the ground pin The CapSense sensors are assigned to the side of the chip that does...

Страница 71: ...CapSense application the capacitive sensors are formed by the traces of a printed circuit board PCB or flex circuit Following CapSense layout best practices will help your design achieve higher noise immunity lower CP and higher signal to noise ratio SNR The CapSense signal drops off at high CP levels due to drive limits of the internal current sources that are part of the CapSense circuitry The l...

Страница 72: ... Button Design The best shape for buttons is round Rectangular shapes with rounded corners are also acceptable Because sharp points concentrate fields avoid sharp corners less than 90º when designing your sensor pad Figure 3 49 Recommended Button Shapes Button diameter can range from 5 mm to 15 mm with 10 mm being suitable for the majority of applications A larger diameter helps with thicker overl...

Страница 73: ...er requires that a slider design be such that whenever a finger is placed anywhere between middle of segment SLD0 and middle of segment SLDn 1 other than the exact middle of slider segments exactly two sensors report a valid signal3 If finger is placed at the exact middle of any slider segment the adjacent sensors should report difference count noise threshold Therefore it is recommended to use a ...

Страница 74: ...approximately 9 mm Based on this average finger diameter and Equation 3 25 the recommended slider segment width and air gap is 8 mm and 0 5 mm respectively If the slider segment width 2 air gap is lesser than finger diameter as required per Equation 3 25 the centroid response will be non linear This is because in this case a finger placed on the slider will add capacitance and hence valid signal t...

Страница 75: ...near by the maximum position Figure 3 54 Nonlinear Centroid Response when Slider Segment Width Is Lower Than Recommended Note that even though a slider segment width value of less than finger diameter 2 air gap provides a non linear centroid response as Figure 3 53 shows it may still be used in an end application where the linearity of reported centroid versus actual finger position does not play ...

Страница 76: ...r segment width 2 air gap is higher than finger diameter as required per Equation 3 25 the centroid response will have flat spots i e if the finger is moved a little near the middle of any segment the reported centroid position will remain constant as Figure 3 57 shows This is because as Figure 3 58 shows when the finger is placed in the middle of a slider segment it will add valid signal only to ...

Страница 77: ... one segment is scanned the adjacent segments are connected to either ground or to the driven shield signal based on the option that will be specified in the Inactive sensor connection parameter in the CapSense CSD component For linear centroid response the slider requires all the segments to have same sensitivity i e the increase in the raw count signal when a finger is placed on the slider segme...

Страница 78: ...ased on application requirements This is same as the effective slider length as Figure 3 50 shows b Decide the height of segment based on available space on the board Use maximum allowed segment height 15 mm if board space permits else use a lesser height but ensure that the height is greater than the minimum specified in Table 3 9 c The slider segment width and the air gap between slider segments...

Страница 79: ...You can either place the LEDs just above the slider segments or drill a hole in the middle of a slider segment for LED backlighting as Figure 3 60 shows When a hole is drilled for placing an LED the effective area of the slider segment reduces To achieve an SNR 5 1 you need to have a slider segment with a width larger than the LED hole size Refer to Table 3 9 for minimum slider width required to a...

Страница 80: ...CB traces Do this by placing them at least 4 mm apart and fill a hatched ground between CapSense traces and non CapSense traces to avoid crosstalk Avoid connectors between the sensor and the controller pins because connectors increase CP and decrease noise immunity 3 8 7 Trace Length and Width Minimize the parasitic capacitance of the traces and sensor pad Trace capacitance is minimized when they ...

Страница 81: ...1X34 B the crosstalk can also occur due to the coupling of the LED voltage transitions with the RB resistor To avoid this isolate the RB trace from the non CapSense traces A minimum separation of 4 mm is recommended A hatched ground plane also can be placed between those traces to isolate them LED drive traces and CapSense traces including RB trace should not be routed together Figure 3 64 Not Rec...

Страница 82: ...ensors to go off unintentionally when the LEDs change state To avoid the effect of LEDs that are placed close to the sensors the LEDs must be bypassed with a capacitor with a typical value of 1 nF This is important in scenarios where LEDs are pulled down or pulled up to switch on and are left floating when switched off The value of the bypass capacitor must be such that it provides a constant low ...

Страница 83: ...ut Recommendations A poor PCB layout would introduce noise in high sensitivity sensors e g proximity sensors and button sensors that use overlays thicker than 1 mm To achieve low noise on high sensitivity CapSense sensors in designs it is important that the PCB layout follows the best practices on power supply trace and placement 1 Two decoupling capacitors must be connected between the VDD and VS...

Страница 84: ...ws an example board layout diagram with placements of decoupling and CMOD capacitors and routing of ground and supply Note that the I2 C pull ups present in Figure 3 71 are not shown in the layout in this figure Figure 3 72 Example Board Layout for Improved SNR A good CapSense schematics diagram must have all passive components shown in the schematics diagram The PCB layout shown above is for guid...

Страница 85: ...gure 3 42 Provide directionality to proximity sensing The electric field of a proximity sensor is omnidirectional and can detect proximity in all directions In most of the applications it is required to detect proximity from only one direction In such cases you can use a shield electrode to make the proximity sensor sense the target object in a single direction Provide liquid tolerance As explaine...

Страница 86: ... a shield electrode in between the sensor and ground the effect of shield electrode will be totally masked out and sensors might false trigger In some applications there might not be sufficient area available on the PCB for shield electrode implementation In such cases the shield electrode can spread less than 1 cm and the minimum area for shield electrode can be the area remaining on the board af...

Страница 87: ...s for implementing the guard sensor The guard sensor should be in the shape of a rectangle with curved edges and should surround all the sensors The recommended thickness for a guard sensor is 2 mm The recommended air gap between the guard sensor and the shield electrode is 1 mm If there is no space on the PCB for implementing a guard sensor the guard sensor functionality can be implemented in the...

Страница 88: ...ensor shape recommended in section Button Design for button sensors and section Slider Design for slider sensors applies to the sensor design on ITO Make sure that the sensor length or width where length is the always the longest dimension aspect ratio does not exceed 5 3 Trace length for the sensors should be kept at minimum to reduce the overall sensor resistance The formula for trace resistance...

Страница 89: ...hoose programmable controllers if you need more integration in one chip and more flexibility in designing your application Cypress offers both hardware configurable and register configurable controllers Configuration Interface Configurable controllers have two configuration interfaces hardware based and register based Hardware configurable controllers require external resistors for configuring dif...

Страница 90: ...t if your CapSense design involves a host controller This interface will allow the host controller to configure the device and get the user interface data in the system I2 C is a popular interface in capacitive touch sensing applications Cypress controllers support I2 C SPI and UART depending on the device CPU Flash and RAM requirements ARM is the popular CPU choice for embedded applications as it...

Страница 91: ... for environmental changes during runtime The parasitic capacitance CP supported by these devices is limited to 45 pF CY8CMBR3XXX controllers are the third and latest generation of configurable controllers that can be configured over I2 C and are supported by the GUI based configuration tool EZ Click These devices support up to 16 buttons up to eight LEDs up to two proximity sensors up to two 5 se...

Страница 92: ...p to 16 Up to 10 Up to 10 Up to 4 Up to 10 Sliders No Up to 2 No No No No No No No No 1 Proximity Up to 2 Up to 2 Up to 2 Up to 2 Up to 2 No No No No No No Liquid Tolerance Yes No LED GPO Up to 8 0 Up to 5 Up to 4 Up to 1 2 Up to 8 Up to 10 Up to 10 Up to 4 Up to 10 Buzzer Yes Yes Yes Yes No No Yes Yes No No No Configuration Interface I2C I2C I2C I2C I2C No Fixed Function Hardware I2C Hardware Har...

Страница 93: ...LP supports up to 62 sensors and is suitable for large and complex systems that need higher levels of integration in a single chip Table 4 4 shows the comparison between the different PSoC 5LP sub families PSoC 3 family features a 8 bit single cycle 8051 CPU clocked up to 67 MHz and integrates many advanced peripherals such as a 20 bit delta sigma ADC 8 bit DAC opamps comparators PWM USB 2 0 Full ...

Страница 94: ...p to 256 KB Up to 32 KB Up to 32 KB Up to 4 KB Up to 64 KB Up to 8 KB For PSoC 4100PS Up to 32 KB Up to 4 KB Up to 128 KB Up to 16 KB Total I Os Up to 20 Up to 36 Up to 36 Up to 55 Up to 55 Up to 36 Up to 36 Up to 98 Up to 36 Up to 36 Up to 38 For PSoC 4100PS Up to 54 CapSense I Os Supports Button Slider Proximity Shield Up to 16 Up to 35 Up to 35 Up to 54 Up to 54 Up to 35 Up to 35 Up to 97 Up to...

Страница 95: ...No No No No No No Up to 4 Channels For PSoC 4100PS only No Voltage DAC VDAC No No No No No No No No No No 13 bit VDAC For PSoC 4100PS only No Serial Communication Block SCB12 1 I2C only13 2 2 4 4 2 2 4 2 3 5 Universal Digital Block UDB14 0 0 Up to 4 0 4 0 4 8 0 0 0 10 CapSense block is repurposed as an ADC to measure the input voltage of 0 5 V with the result in mV When this ADC is used CapSense i...

Страница 96: ...rgy BLE No Yes No No No No CAN 2 016 No No No No Yes No No Yes No No Yes USB No No No No No No No Yes No No No Operating Voltage 1 71 5 5 V Automotive Qualified AEC Q100 17 Yes No Package 8 16 pin SOIC 16 24 pin QFN 28 pin SSOP 16 pin WLCSP18 28 pin SSOP 40 pin QFN 44 pin TQFP 48 pin LQFP 35 pin WLCSP18 48 pin TQFP 64 pin TQFP 68 pin QFN 56 pin QFN 68 pin WLCSP18 76 pin WLCSP18 124 BGA 68 QFN 64 p...

Страница 97: ... Universal Digital Block UDB20 Up to 24 16 bit Timer PWM 4 Digital Filter Block DFB21 No No Yes Yes Segment LCD Drive Up to 46x16 segments USB 2 0 Full Speed Peripheral Yes CAN 2 022 No No Yes Yes Package 68 pin QFN 100 pin TQFP 99 pin WLCSP23 Automotive Qualified AEC Q100 No Operating Voltage 1 71 5 5V 19 Switched Capacitor Continuous Time blocks which are programmable to work as Opamp Unity Gain...

Страница 98: ...FB26 No No Yes Yes Segment LCD Drive Up to 46x16 segments USB 2 0 Full Speed Peripheral Yes CAN 2 027 No Yes Yes Yes Operating Voltage 1 71 5 5V Automotive Qualified AEC Q100 No Package 48 pin SSOP 48 pin QFN 68 pin QFN 100 pin TQFP 72 pin WLCSP28 48 pin SSOP 48 pin QFN 68 pin QFN 100 pin TQFP 48 pin SSOP 48 pin QFN 68 pin QFN 100 pin TQFP 72 pin WLCSP28 48 pin SSOP 48 pin QFN 68 pin QFN 100 pin T...

Страница 99: ... bit 8 bit Up to 9 bit Amplifiers Yes Yes I2C Master and Slave Interface SPI UART Transmitter Software UART Transmitter Software Transmitter Software UART UART UART Transmitter Software USB Full Speed USB Full Speed USB Timer 16 bit timer 8 to 32 bit timer counter 16 bit timer 16 bit timer 8 to 32 bit timer counter 8 to 32 bit timer counter 8 to 32 bit timer counter 13 bit timer PWM 8 to 32 bit de...

Страница 100: ...procedures for running the code examples Select a CapSense Part 1 Refer to the CapSense Selector Guide section in this guide 2 Once you have selected a part refer to the device specific Design Guide to help with your design Design CapSense Hardware 1 Watch the CapSense layout best practices videos Part 1 and Part 2 2 Refer to the device specific Design Guide for schematic layout and overlay design...

Страница 101: ...nsing 1 In this document you can learn about Proximity Sensing 2 Evaluate proximity sensing using CY8CKIT 024 CapSense Proximity Shield along with a PSoC 4 pioneer kit 3 Refer to Design CapSense Hardware section in this table above to help with your schematic and layout design 4 Explore additional information on proximity design guidelines AN92239 Proximity Sensing with CapSense This application n...

Страница 102: ...E and PRoC BLE Over The Air OTA Device Firmware Upgrade DFU Guide AN2100 Bootloader PSoC 1 For programming through a dedicated programming interface AN84858 PSoC 4 Programming Using an External Microcontroller AN73054 PSoC 3 and PSoC 5LP Programming Using an External Microcontroller AN44168 PSoC 1 Device Programming using External Microcontroller AN59389 Host Sourced Serial Programming for CY8C20x...

Страница 103: ... Design Guide CapSense Express CY8C201XX Application Notes Design Guides for PSoC 1 Devices CY8C20XX7 S Design Guide CY8C20XX6A H CapSense Design Guide CY8C21X34 B CapSense Design Guide CY8C20X34 CapSense Design Guide Getting Started Application Notes for PSoC 1 PSoC 3 PSoC 4 and PSoC 5LP AN75320 Getting Started with PSoC 1 AN54181 Getting Started with PSoC 3 AN79953 Getting Started with PSoC 4 AN...

Страница 104: ...age under Design Support as shown in Figure 5 1 Use the search box at the top right of Cypress website to search for a resource Select the type of collateral you want and type in your key words as shown in Figure 5 2 Figure 5 1 Design Support in Cypress Website Figure 5 2 Cypress Web Search ...

Страница 105: ...PSoC 1 systems Develop your applications using a library of pre characterized analog and digital peripherals in a drag and drop design environment Then customize your design leveraging the dynamically generated API libraries of code Figure 5 4 shows the PSoC Designer windows Note This is not the default view 1 Global Resources all device hardware settings 2 Parameters the parameters of the current...

Страница 106: ...ct Model COM Interface Guide available under Program Files x86 Cypress Programmer Documents folder for more details PSoC Creator and PSoC Designer provide in window programming interface that in turn invokes the PSoC Programmer APIs 5 3 2 Data Monitoring Tools These tools help you to debug monitor and tune CapSense designs For more details on the tools see the application note AN2397 CapSense Data...

Страница 107: ...8CKIT 046 Pioneer Kit for PSoC 4 L Series devices CY8CKIT 041 Pioneer Kit for PSoC 4 S Series devices 5 4 1 2 Shield Kits Shield kits are designed to be Arduino compatible and to work with the PSoC Pioneer kits CY8CKIT 022 CapSense Liquid Level Sensing Shield CY8CKIT 024 CapSense Proximity Shield 5 4 1 3 Prototyping Kits Prototyping Kits are low cost platforms for prototyping products using PSoC 4...

Страница 108: ...Miniprog3 The CY8CKIT 002 PSoC MiniProg3 Program and Debug Kit is an all in one programmer for PSoC 1 PSoC 3 PSoC 4 and PSoC 5LP architectures a debug tool for PSoC 3 PSoC 4 and PSoC 5LP architectures and a USB I2C Bridge for communicating with PSoC devices Other than for programming this device is mainly used as a USB to I2C Bridge in data monitoring and tuning of CapSense solutions 5 4 5 2 CY321...

Страница 109: ...ngs Influence of overlay thickness on Finger Touch added Capacitance FTC with springs is similar to that with solid sensors Figure 5 6 FTC Versus Overlay Thickness Influence of height on FTC Figure 5 7 FTC Versus Spring Height 0 0 2 0 4 0 6 0 8 1 1 2 0 2 4 6 8 10 12 Thickness of the Overlay mm Introduced Capacitance pF Spring Solid Sensor 0 0 1 0 2 0 3 0 4 0 5 0 6 0 5 10 15 20 25 30 35 Height of t...

Страница 110: ...Versus Spring Diameter Influence of wire thickness of the spring on FTC Figure 5 9 FTC Versus Wire Thickness of Spring 0 0 5 1 1 5 2 2 5 3 0 5 10 15 20 25 Diameter of the Spring mm Introduced Capacitance pF 0 52 0 53 0 54 0 55 0 56 0 57 0 58 0 59 0 1 2 3 4 5 6 Wire Thickness of the Spring mm Introduced Capacitance pF ...

Страница 111: ...r 3 times The distance between the PCB and the overlay must be 5 mm or more Figure 5 10 Spring Mounting Example PCB Metal Spring Trace to PSoC Solder VIA Overlay VIA Solder Point Copper Ring Trace to PSoC Metal Spring PCB LED for BackLighting VIA Sensing Area Copper free area 5 m m Overlay Figure 5 11 shows examples of footprints for springs Unlike a button sensor which is a copper pad on the PCB ...

Страница 112: ...s the sensor while pressing the button activates both the sensor and mechanical button In this case preparatory actions such as backlighting prompt showing and others are possible only if the sensor works The final action is performed when both buttons work For example in a GPS navigation system touching a button shows only a hint and pressing the button takes an action A 3 Design Examples Figure ...

Страница 113: ...Springs AN64846 Getting Started with CapSense Doc No 001 64846 Rev X 113 Figure 5 14 Cooktop Front Panel ...

Страница 114: ...ecoupling Capacitor Refer to Power Supply Layout Recommendations for complete details B 1 2 Bulk Capacitor Refer to Power Supply Layout Recommendations for complete details B 1 3 Pin Assignment Distribute the LEDs evenly among even and odd pins such as P2 0 P2 2 and P2 1 P2 3 Try not to keep LEDs next to CapSense pins Reserve pins for RB if required CMOD and Shield tank capacitors if required It i...

Страница 115: ...C21x34 SmartSense 15 kΩ B 1 6 Series Resistor on CapSense Lines A 560 ohm resistor on CapSense signal lines If the series resistance value is set larger than 560 ohms the slower time constant of the switching circuit limits the amount of charge that can transfer This lowers the signal level which in turn lowers SNR Smaller values are better but are less effective at blocking RF For complete detail...

Страница 116: ...ectric constant except conductors There should be no air gap between sensor board and overlay Front panel of the casing Thickness for acrylic overlay 5 mm Thickness for glass overlay 15 mm Overlay thickness should be low This is applicable to both buttons and sliders For proximity sensors thicker overlays increase the capacitance coupled with human hand finger and the sensor and hence increases th...

Страница 117: ...re 3 49 for details Size can range from 5 mm to 15 mm Go for larger diameter for thicker overlays Air gap to ground and other sensors should be equal to the overlay thickness but no smaller than 0 5 mm and no larger than 2 mm The spacing between the two adjacent buttons should be large enough that if one button is touched a finger should not reach the air gap of the other button Placement near any...

Страница 118: ...Refer Trace Routing for details Route sensor traces on the bottom layer of the PCB Do not run traces underneath a sensor unless the sensor and the trace are connected Do not route sensor traces in parallel to noisy clock and LED lines Use ground or shield around sensor traces for shielding Do not run sensor traces in close proximity to communication lines such as I2C or SPI masters If it is necess...

Страница 119: ...apacitor filter between the shield electrode port pin and ground will reduce slew rate Put a small value of series resistor For more details on shield design considerations for emission reduction refer to Shield B 2 9 Guard Sensor a The shield electrode should surround the guard sensor pad and exposed traces and spread no further than 10 mm from these features b The recommended shape for a guard s...

Страница 120: ...strated in Figure C 2 The parasitic capacitance of the sensor Cp is related to this electric field Figure C 1 CapSense Board Top and Bottom Layer Figure C 2 Button Ground Plane Fringing Fields Button Ground Ground The capacitance CP decreases as the clearance surrounding the button increases An example of this dependence of CP on the gap is shown in Figure C 3 through Figure C 6 In these plots the...

Страница 121: ...ance increases with sensor size but decreases with the gap The capacitance Csensor is the total sensor capacitance when the finger is not on the sensor It includes the effect of the sensor pad the traces and vias Figure C 4 shows the sensor capacitance for a board routed with 50 mm trace length 8 mil 0 3 mm trace width and 20 mil 0 8 mm spacing from trace to the coplanar ground Figure C 4 Sensor C...

Страница 122: ...te The finger is on the sensor Capacitance increases with both sensor size and gap Figure C 6 plots finger capacitance as a percentage of the sensor capacitance This is the sensitivity of the sensor The sensitivity of the system changes with the routing of the CapSense traces For example increasing the trace length between the PSoC and the sensor pad decreases the button s sensitivity Figure C 6 S...

Страница 123: ...DK ICE kit via a flex cable and the target PSoC device in a prototype system or PCB via package specific pod feet The user guide and the quick start guide for the ICE kit are available here Following are the pods available Note that some of the following pod kits are not in stock but a web page is kept for accessing the documents Contact Cypress technical support if you need help with a particular...

Страница 124: ...nd substrate such as a copper button on a printed circuit board PCB which reacts to a touch or an approaching object with a change in capacitance CapSense Cypress s touch sensing user interface solution which is the industry s leading solution in sales CapSense Mechanical Button Replacement MBR Cypress s configurable solution to upgrade mechanical buttons to capacitive buttons It requires minimal ...

Страница 125: ...ging in firmware that is multiple sensors can be connected simultaneously to AMUXBUS for scanning Gesture Gesture is an action such as swiping and pinch zoom performed by the user CapSense has a gesture detection feature that identifies the different gestures based on predefined touch patterns In the CapSense component the Gesture feature is supported only by the Touchpad Widget Guard Sensor Coppe...

Страница 126: ...tor output in a CSD block to maintain the AMUXBUS voltage at VREF The average current supplied by this IDAC is equal to the average current drawn out by the sensor capacitor Mutual Capacitance Capacitance associated with an electrode say TX with respect to another electrode say RX is known as mutual capacitance Negative Noise Threshold A threshold used to differentiate usual noise from the spuriou...

Страница 127: ...r is dependent on the board layout overlay properties sensing method and tuning parameters Sense Clock A clock source used to implement a switched capacitor front end for the CSD sensing method Sensor See Capacitive Sensor Sensor Auto Reset A setting to prevent a sensor from reporting false touch status indefinitely due to system failure or when a metal object is continuously present near the sens...

Страница 128: ...ific horizontal and vertical fashion to detect the X and Y position of a touch Trackpad See Touchpad Tuning The process of finding the optimum values for various hardware and software or threshold parameters required for CapSense operation VREF Programmable reference voltage block available inside PSoC used for CapSense and ADC operation Widget A user interface element in the CapSense component th...

Страница 129: ...pdated Section 3 1 Added Section 3 7 13 I 03 07 2013 ZINE Updated Section 2 7 2 Haptic Feedback J 06 07 2013 DST Added the CY8C20XX7 S part family Added proximity information K 09 04 2013 TEJU Added the CY8C22X45 part family information L 10 04 2013 LPG Corrected document revision on the footer of some pages M 02 19 2014 SSHH Added information specific to CY8CMBR3XXX N 03 05 2014 SHAS Updated the ...

Страница 130: ...n CapSense Updated Figure 4 1 to add cortex M0 for PSoC 4000S and PSoC 4100S family of devices Updated Table 4 3 PSoC 4 Family Features Comparison with PSoC 4200 L PSoC 4000S and PSoC 4100S family of devices details Updated PSoC 4 Development Kits with PSoC 4 Pioneer Kits and Shield Kits T 02 24 2016 VAIR Updated Table 5 1 CapSense Resources Navigator Added reference to AN210998 AN96475 U 10 26 20...

Отзывы:

Нет отзывов

Бренды по названию

Популярные бренды

Загрузить еще бренды