ABB SPAM 150 C, Техническая информация

Страница: 20 / 24

20
Solving the equation for heating up with refer-
ence to trip time gives:
t
≈
32.15 x t
6x
x ln
In the above expression I
t
is the trip current level,
which is always 1.05 x I
θ
, i.e.:
t
≈
32.15 x t
6x
x ln
{ }
Appendix 3
Mathematical
equations for
the thermal unit
Heating up during an overload condition:
Θ
A
= (I / (1.05 x I
θ
))
2
x (1-e
-t/
τ
) x 100%
Θ
B
= (I / (1.05 x I
θ
))
2
x (1-e
-t/
τ
) x p%
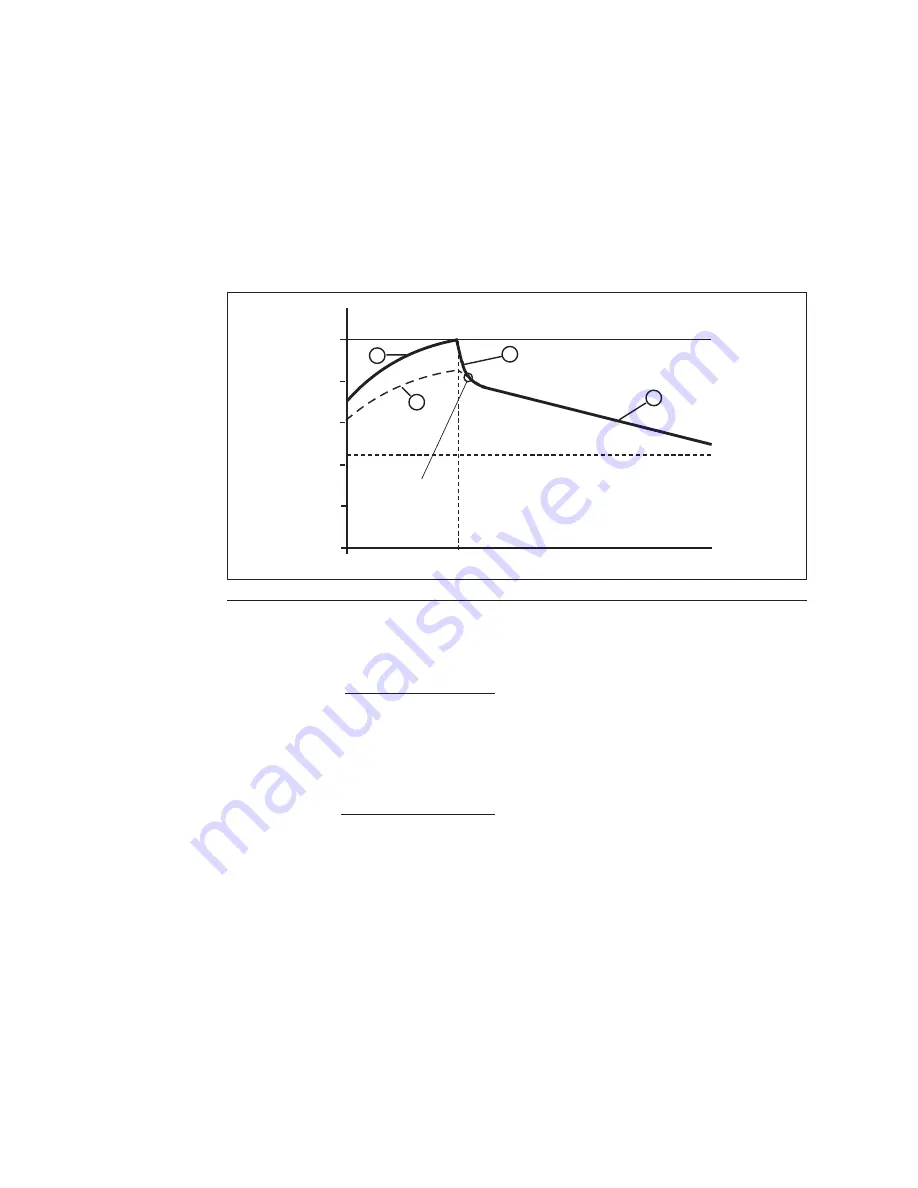
Cooling at normal load or in a standstill condi-
tion:
When the current decreases below 1.0 x I
θ
, the
thermal curve A is linearly brought down to
the level of the thermal history curve B as shown
in curve part C. This corresponds to the level-
ling out of the hot spots in the motor.
Thereafter the cooling follows the lower curve
with a time constant equal to the heating time
constant as long as the motor is running at nor-
mal load or idling.
For a motor at standstill, i.e. when the current is
below 12% of I
θ
, the cooling can be expressed
as:
Θ
=
Θ
02
x e
-t/kc x
τ
where
Θ
02
is the initial thermal level and kc is
the cooling time multiplier according to the set
value 1...64.
0
20
40
100
60
80
%
A
B
C
D
Θ
02
Estimated trip time
(modified 2003-04)
The parameters I
θ
, t6x and p are the relay set-
tings, I
p
is the long term prior load and finally I
is the overload current which is finally going to
cause a trip. The operand ln is the natural loga-
rithm (log
e
).
The thermal level is handled twice a second in
the relay, giving a best trip time resolution of
0.5 s.
(I/I
θ
)
2
- p /100 x (I
p
/I
θ
)
2
(I/I
θ
)
2
- I
t
/I
θ
)
2
(I/I
θ
)
2
- p /100 x (I
p
/I
θ
)
2
(I /I
θ
)
2
- 1.1025
{ }