be valid only at a single load impedance, usually 600 or
150 ohms.
It's common to rate a mixer's maximum output in
dBm referenced to 600-ohms, and to treat this rating as
if it were a voltage rating, even though it is actually a
power rating. If a mixer's maximum output is rated at
"+24dBm," the rating really means "12.3 volts" (the
voltage produced by a power level of +24dBm into a
600-ohm load). If you realize that by this rating method,
"+24dBm" means "12.3 volts," (and that "+4dBm"
actually means "1.23 volts," etc.), then you can
accurately interpret the specification. Of course, there
are mixers that will deliver 12.3 volts into a high
impedance, but cannot sustain this voltage with a 600-
ohm load, and such mixers could not be honestly rated
at +24dBm. (NOTE: If the mixer's output impedance is
600 ohms or lower, it should be able to sustain the
rated output voltage into 600-ohm loads.)
One possible way to avoid the common, but
inaccurate, "dBm" output rating method would be
to rate the maximum output of a mixer in dBV. Since
the mixer acts like a voltage source, this would be an
accurate rating regardless of the load impedance. Un-
fortunately, the dBV rating is relatively uncommon in
audio (although it is used for some microphone ratings),
so it would be unfamiliar to most users and therefore
difficult to interpret.
To avoid confusion, we have rated outputs in "dB
(volts)," where the dB value is equal to the voltage
produced by a numerically equal "dBm" rating in a
600-ohm circuit. By this method, "0dB (0.775 volts)"
is exactly the same as "0dBm" for a 600-ohm circuit.
Since it is a voltage rating, however, "dB (volts)" is
accurate regardless of the mixer's load impedance, so
long as the mixer is not overloaded. Also, since the
actual output level, expressed in volts, always follows
the dB rating, it is unlikely that the rating will be mis-
interpreted. By this convention we have not created a
new unit, we have merely endeavoured to avoid the
imprecision of existing, widely used dB ratings.
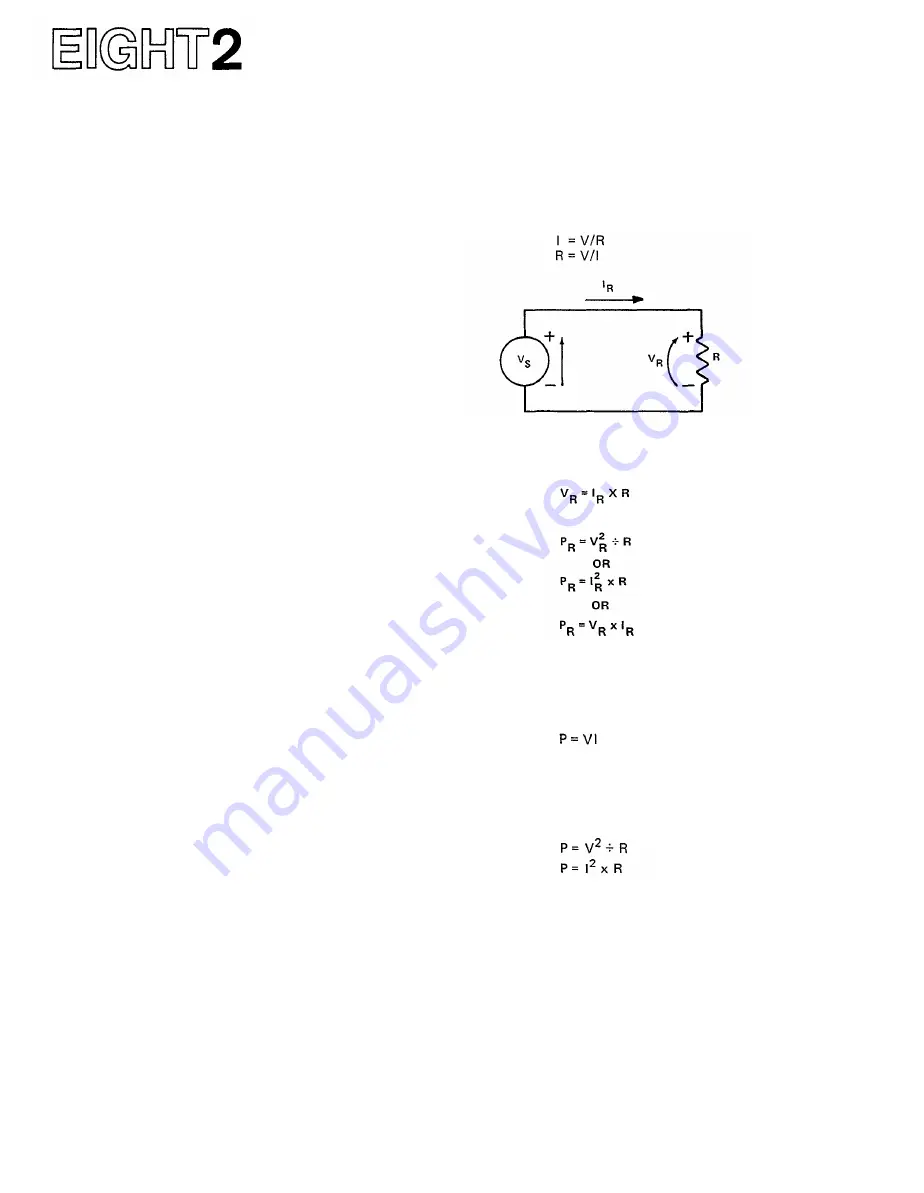
OHM'S LAW
Ohm's law relates voltage, current and resistance in a
DC circuit by the following equation:
V = IR
(Where V is voltage, I is current and R is resistance.)
Other forms of Ohm's law, derived by simple
algebraic manipulation, are:
For this Simple Circuit, the Voltage produced by the Source
V
S
equals the Voltage across the Resistor V
R
The Voltage across and Current through the Resistor are
related by Ohm's law:
The Power Dissipated in the Resistor is:
Fig. 78 - Ohm's Law
POWER
In a DC circuit, the power absorbed by a resistor is
given by the following equation:
(Where V and I are the voltage and current through the
resistor, and P is the power dissipation.)
By using Ohm's law and some algebraic manipulation
again, we come up with two alternate forms of the power
equation:
A "perfect" voltage source would always produce the
same voltage, regardless of the load resistance, and would
be capable of an infinite current into a short circuit
(zero ohms resistance). A "perfect" current source
would always produce the same current, regardless of
the load resistance, and would be capable of an infinite
voltage into an open circuit (infinite ohms resistance, or
no connection).







































