UT3500 series
User Manual
35
6.2 Stat
6.2.1 Process Capability Index
Process capability refers to the ability of process processing to meet processing quality. It
measures the internal consistency of process processing and the smallest fluctuation in
the most stable state. When the process is in a steady state, 99.73% of the product quality
characteristic values are scattered in the interval [
μ
-3
σ
,
μ
+3
σ
]
(
μ
is the overall mean value
of the product characteristic values, and
σ
is the overall standard deviation of the product
characteristic values). Almost all product characteristic values are within the range of 6
σ
.
Therefore, 6
σ
is usually used to represent process capability and the smaller the value,
the better.
Generally
Cp, CpK > 1.33 Process capability is sufficient.
1.00 < Cp, CpK
≦
1.33 Process capability is appropriate.
Cp, CpK
≦
1.00 Process capability is insufficient.
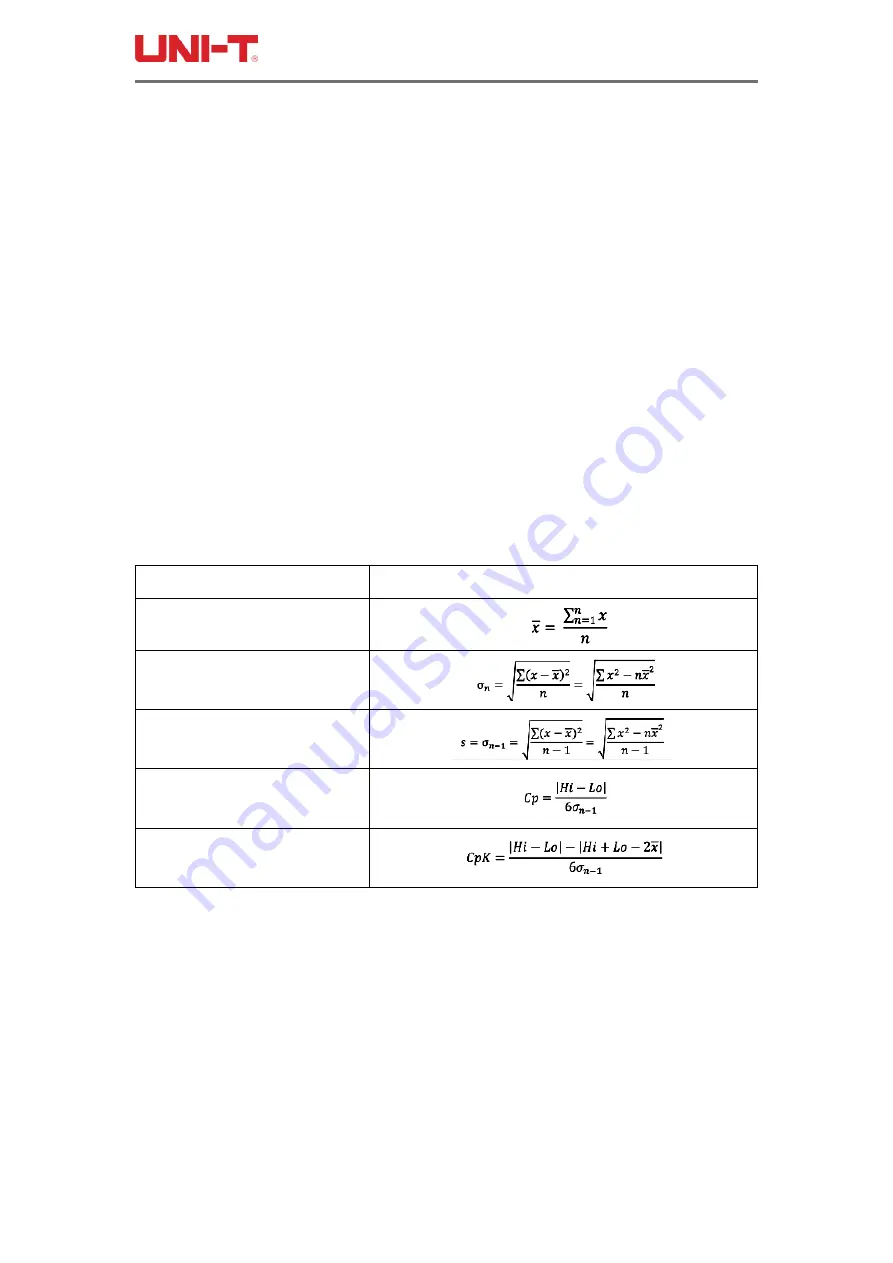
Process capability index and some related formulas:
Process Capability Index
Formulas
Average (Mean)
Population Standard Deviation
σ
n
Sample Standard Deviation
s(=
σ
n-1
)
Process Capability Index
(Deviation) Cp
Process Capability Index
(Offset) CpK
In the above formulas:
a) n represents valid data, that is, the value excluding overflow and open circuit. As long
as the data can be displayed on the screen, they are valid values.
b) Variable Hi and Lo in the Cp and CpK formulas are the actual value of the upper and
lower limits of the comparator. In the PER and ABS comparison mode, the actual value will
be converted from the nominal value. This value will participate in the calculation
regardless of whether the comparator is turned on.
c) When the sample standard deviation
σ
n-1=0, Cp=99.99, CpK=99.99.
d) When CpK <0, CpK = 0.
















































