Trane Tracer MP501, Installation, Operation And Maintenance Manual

Page: 31 / 60

CNT-SVX08F-EN 31
PID Calculations
PID algorithms perform three calculations:
•
Proportional calculation
• Integral calculation
• Derivative calculation.
These calculations are independent of each other, but are combined to determine the response of
the controller to the error.
Proportional Calculation
The proportional calculation responds to how far the measured value is from the setpoint. The
larger the error, the larger the output of the calculation. The proportional calculation has a much
stronger effect on the result of the PID algorithm than either the integral or derivative calculations.
It determines the responsiveness (or aggressiveness) of a control system. Though some systems
use only proportional control, most Trane controllers use a combination of proportional and
integral control.
Proportional-only control loops require an error to produce an output. If the setpoint and the
process variable are the same, the error is zero, so the system does not have an output. In an HVAC
system, this can cause an actuator to open or close. The integral calculation solves this problem.
Integral Calculation
The integral calculation responds to the length of time the measured value is not at setpoint. The
longer the measured value is not at setpoint, the larger the output of the calculation.
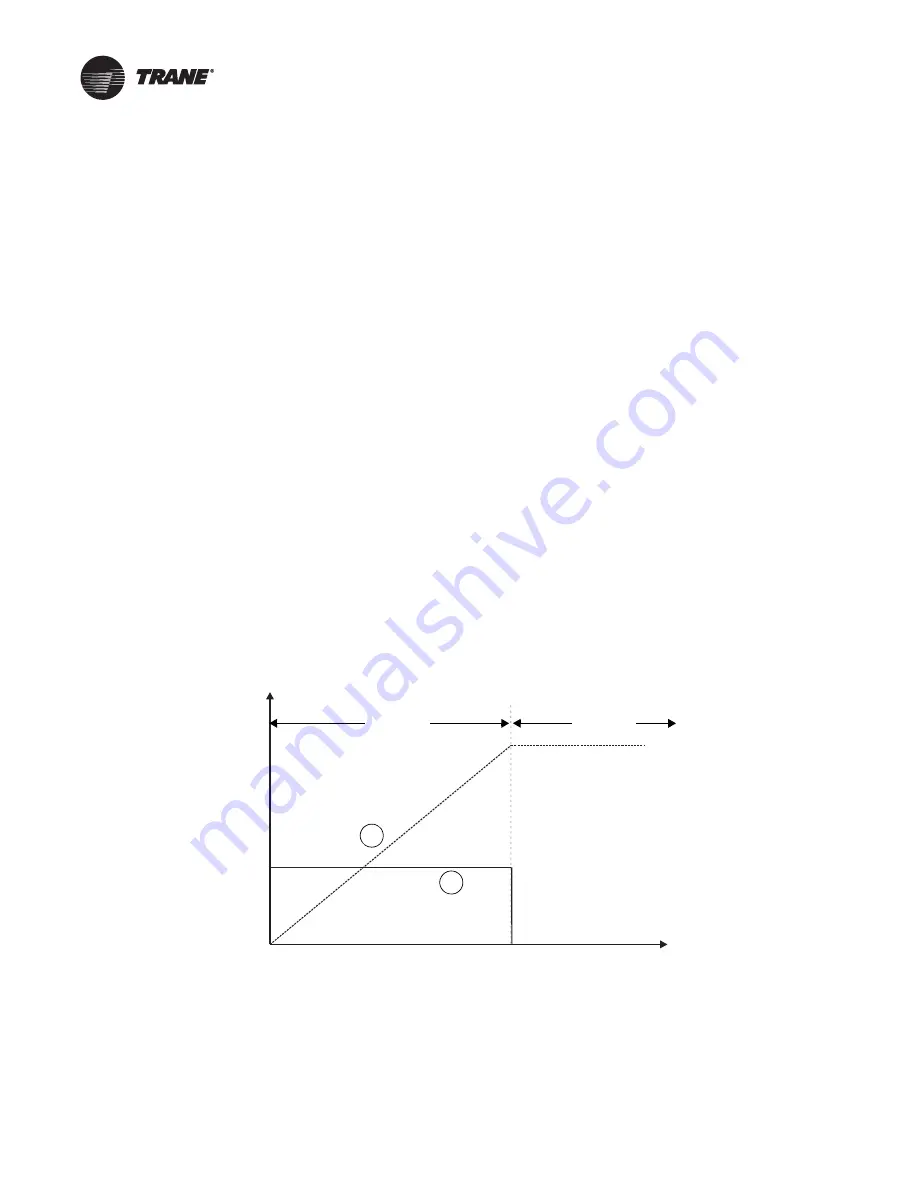
The integral calculation uses the sum of past errors to maintain an output when the error is zero.
Line 1 in
Figure 14 shows that with proportional-only control, when the error becomes zero, the PID
output also goes to zero. Line 2 in Figure 14 shows the integral output added to the proportional
output. Because the integral calculation is the sum of past errors, the output remains steady rather
than dropping to zero when the error is zero. The benefit of this is that the integral calculation keeps
the output at the appropriate level to maintain an error of zero.
Figure 14.
Output
Time
Error

0
Error
= 0
Propor integral
output
Propor integral
output if proportional
output has gone to zero
1
2
Proportional-only
output
Integral output added to proportional output
The value of the integral calculation can build up over time (because it is the sum of all past errors),
and this built-up value must be overcome before the system can change direction. This prevents
the system from over-reacting to minor changes, but can potentially slow the system down.