Assembly Language Programming: Inferential Statistics and Distribution Functions
5
4
Enter the first height value. As
you enter it, it is displayed on
the bottom line.
The value is displayed in the first
row, and the rectangular cursor
moves to the next row. Enter the
other nine height values the
same way.
66
Ë
7
Í
5
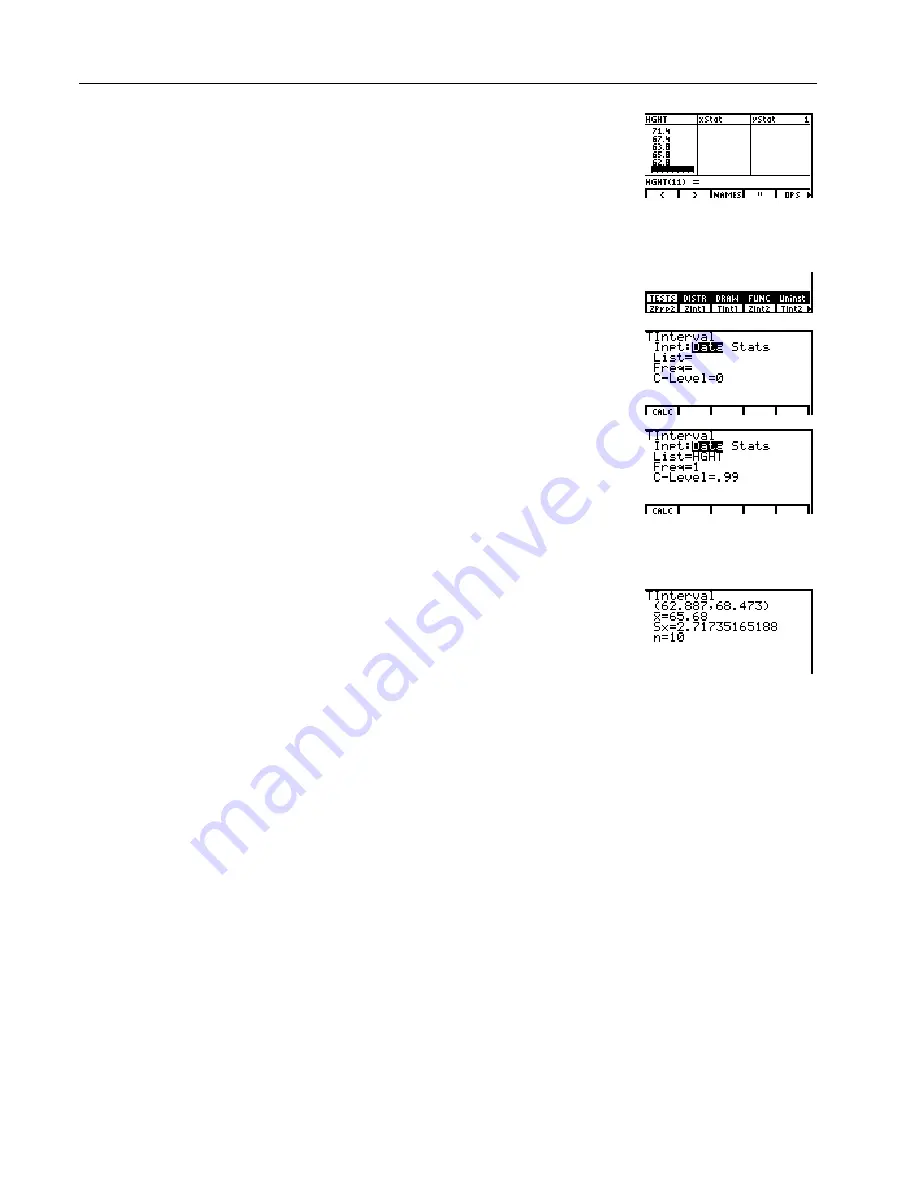
Display the inferential statistics
editor for
TIntl
(
TInterval
) from
the
STAT TESTS
menu.
.
-
Œ
/
'
&
/
(
6
Select
Data
in the
Inpt
field.
If
Stats
is selected,
press
|
Í
7
Enter the test requirements:
¦
Set alpha-lock and enter the
List
name.
¦
Enter 1 at the
Freq=
prompt.
¦
Enter a 99 percent
confidence level at the
C-Level=
prompt.
†
1
1
[H] [G] [H] [T]
†
1
†
Ë
99
8
Calculate
the test. The
results
are displayed on the home
screen.
Note:
Press
.
,
:
, or
b
to clear the results from
the screen.
&
Interpreting the Results
The first line
(62.887,68.473)
shows that the 99 percent confidence interval for the
population mean is between about 62.9 inches (5 feet 2.9 inches) and 68.5 inches
(5 feet 8.5 inches). This is about a 5.6-inch spread.
The .99 confidence level indicates that in a very large number of samples, we
expect 99 percent of the intervals calculated to contain the population mean. The
actual mean of the population sampled is 65 inches, which is in the calculated
interval.
The second line gives the mean height of the sample
þ
used to compute this
interval. The third line gives the sample standard deviation
Sx
. The bottom line
gives the sample size
n
.
To obtain a more precise bound on the population mean
m
of women’s heights,
increase the sample size to 90. Use a sample mean
þ
of 64.5 and sample standard
deviation
Sx
of 2.8 calculated from the larger random sample. This time, use the
Stats
(summary statistics) input option.




















