Shimadzu IRAffinity-1, Instruction Manual

Page: 27 / 134

1.2 Resolution and Apodization
1-5
IRAffinity-1
Although Equation 1.4 maintains that the interferogram should be recorded from -
∞
to +
∞
, such limits are
impractical. In reality, the integration is limited to an optical path difference L, determined by the range of the
moving mirror. The experimental spectrum B'(
σ ) differs from the theoretical spectrum B( σ ) accordingly.
According to Convolution Theory,
Where F(
σ
) is a Fourier transform of the function A(
χ
) in Equation 1.6.
The measured spectrum B'(
σ
) is a convolution of theoretical spectrum B(
σ
) with F(
σ
). F(
σ
), a Fourier transform
of A( χ ), is called instrument function or instrumental line shape ILS.
Functions A(
χ
) and F(
σ
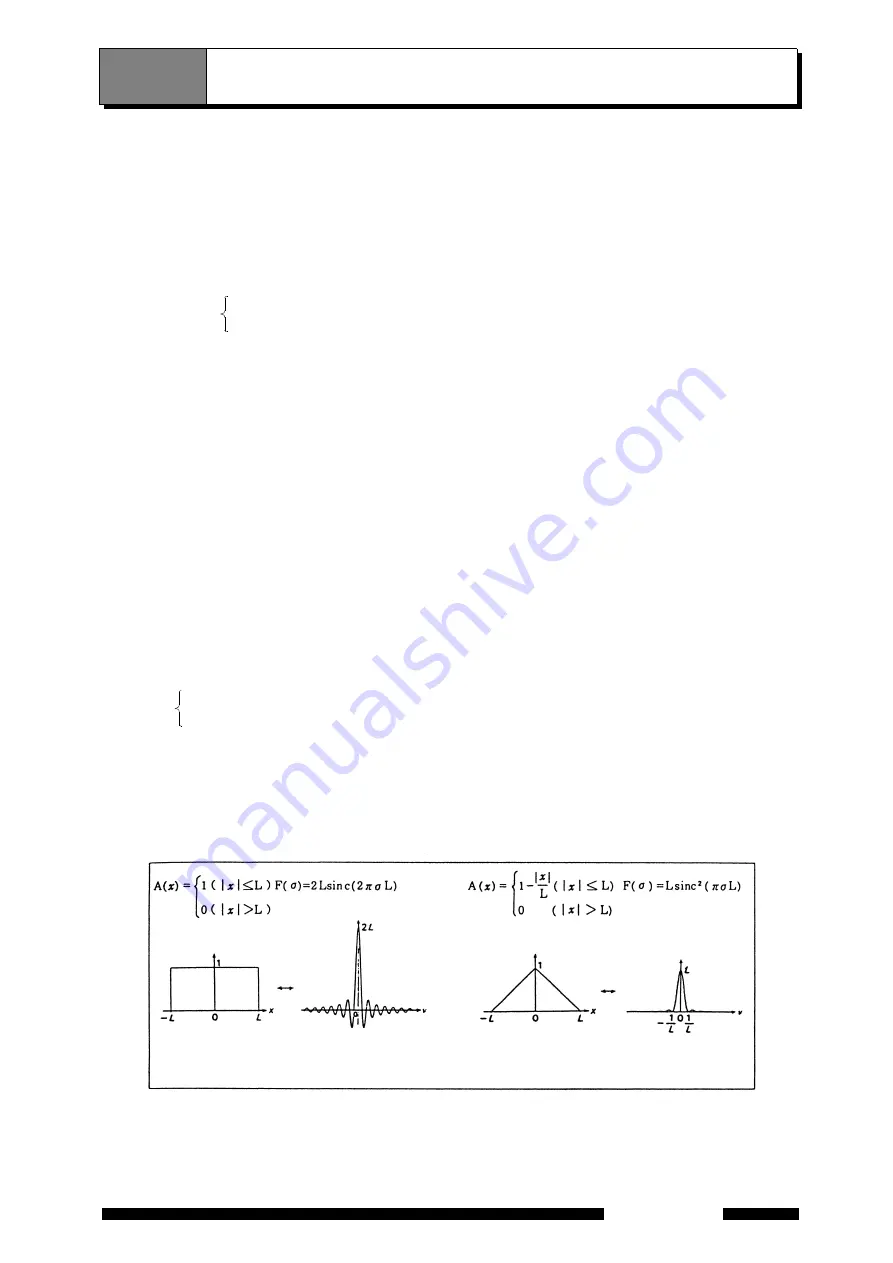
), represented by Equations 1.6 and 1.8 respectively, are given in Fig. 1.3 (a). The
function F( σ ), as defined by Equation 1.8, first becomes zero at ( = ± (1/2L), where the half-width value is 0.605/
L. The greater the optical path difference L, the smaller the half-value width; when the moving mirror is driven
further, the resolution improves.
The instrument function F(
σ
) involves marked submaxima, called side-lobes [ Fig. 1.3 (a)]. If A(
χ
), as defined by
1.6, is replaced by the triangular function defined by 1.9, Equation 1.10 gives its Fourier transform.
Fig. 1.3 (b) illustrates that the instrument function defined by 1.10 has worse separation, but smaller
submaxima, than that defined by 1.8. Using A(
χ
) to reduce the instrument function submaxima called
apodization; A( χ ) is called the apodization function.
Fig. 1.3 Apodization with "Rectangular" and "Triangular" Functions
1.2 Resolution and Apodization
B ′ σ ( ) I χ ( ) 2 πσχ cos χ d
L –
L
∫
=
A
χ ( )
I
χ ( )
2
πσχ
cos
χ
d
∞ –
+ ∞
∫
=
........................................................................................................... (1.5)
where A
χ ( )
1 if χ ( ) L ≤
0 if
χ ( )
L
>
=
................................................................................................................... (1.6)
B ′ σ ( ) B σ ( )∗ F σ ( ) = ................................................................................................................................... (1.7)
............................................................................................................................. (1.8)
F (
σ
) = 2L sin (2
πσ
L)/(2
πσ
L)
= 2L sin χ (2 σ L)
............................................................................................................... (1.9)
............................................................................................... (1.10)
A(
χ
) =
1 − | χ /L| for | χ | ≤ L
0 for |
χ
| > L
F( σ ) = Lsin
2
( πσ L)/( πσ L)
2
= Lsin χ
2
( σ L)
(a) "Rectangular" function (b) "Triangular" function