© Pro-ject Audio Systems · Pro-Ject Align it PRO· Revision 2022.10.07
5
Technical Deep Talk: Tonearm geometry, Baerwald and null-points
The optimum geometry of tonearms has been the subject of several articles over the past decades. However,
the earliest complete mathematical study was that of H.G. Baerwald in his paper on optimum geometry in
1941, where an analytical survey of tracking error distortion showed that optimum geometry of a tonearm of
given effective length would have a corresponding offset angle and overhang. This seems obvious today, but
H.G. Baerwald was the first to show these facts.
Problems with playback in the inner grooves
The RIAA standard for 12" (long play records) says that the "Minimum Inside Diameter of Recording" is 4 3/4",
which means a diameter of 120,65mm or a better radius of 60,325mm. Stopping groove (closed concentric
circle) should be on the diameter of 4 3/16
”
± 1/32
”
. This means a diameter of 106,36mm or a radius of
53,18mm. Unfortunately, today most record publishers don't follow RIAA standards for records and cut the
grooves very close to the stopping track. Very often nowadays, the end of the recording is found at a radius of
55mm. This allows the record to hold more music, but on the other side, it has very serious consequences.
1. A record player has constant angular speed, but as the radius of the grooves decreases, it also decreases
the linear distance the cartridge travels in the groove in a given time. On the outer groove the linear velocity
is 509mm/sec. On a groove with a radius of 60,325mm the linear velocity is 210mm/sec; on a radius of
55mm, it drops to only 190mm/sec. So, if the signal of 10kHz has a "length" of 0,05mm on the outer groove,
on the inner groove with radius of 60mm, it will be only 0,02mm, and on 55mm, it will be 0,018mm. This is
precisely the radius of the classical spherical stylus. But also, an elliptical stylus will have the problem of playing
back such signal in case it is not perfectly aligned.
2. Tracking error versus radius of the groove versus distortion:
Bearing in mind that distortion = ABS((50 x tracking error)/groove radius), we can easily calculate that a
tracking error of 2 degrees will generate outer groove distortion = ABS((50 x 2)/146) = 0,684%, but the same
tracking error of 2 degrees on radius of 55mm will be already = ABS((50 x 2)/55) = 1,81%. So, the same
tracking error generates three times higher distortion on the radius of 55mm than on radius of 146mm.
Bearwald (null points 66,0 and 120,9 mm)
Also known as Lofgren A, minimizes and equalizes distortion at the three weighted tracking error peaks resulting
in a good compromise between inner and outer groove tracking. Baerwald displays moderate distortion at the
beginning of the record, quite low distortion in the area between the null-points, but a steep increase in
distortion from inner null-points up to the most inner groove. An excellent starting point and works universally
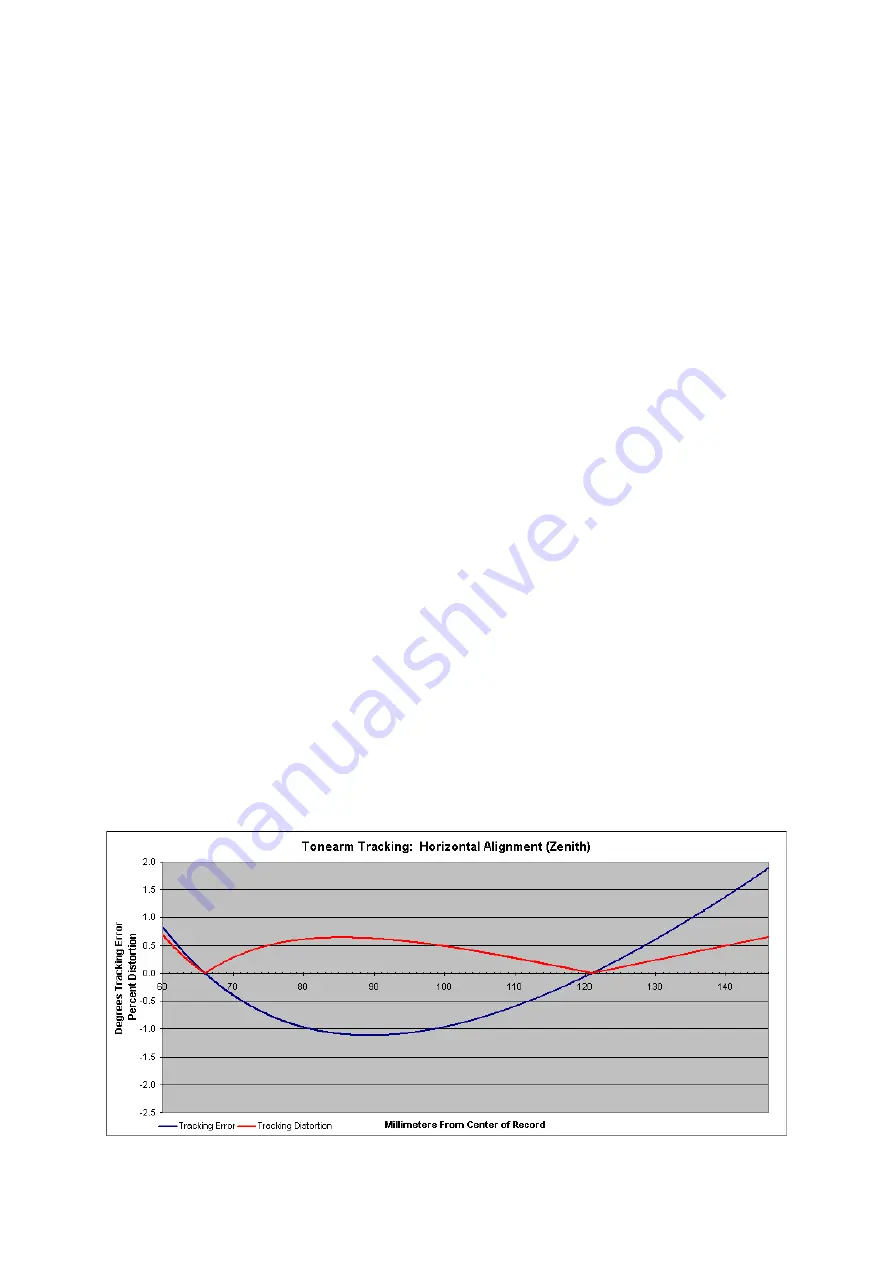
well for many musical tastes. Widely used in the industry, null-points at 66,0 and 120,9 mm. Here is an
example of the typical Baerwald geometry with correct null points. The blue curve shows the tracking error.







