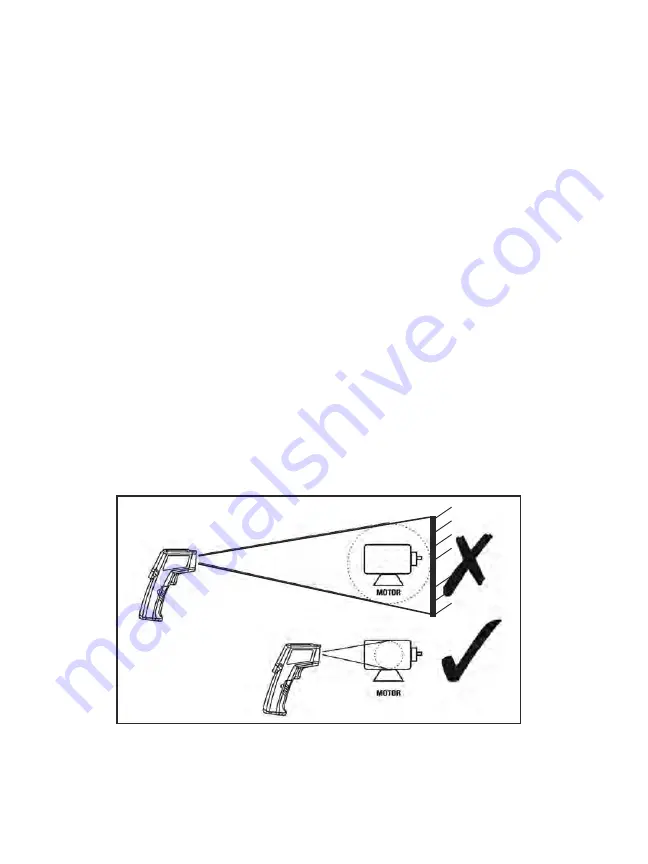
To explain the relationship between D:S ratio and measurement accuracy, consider how
the OS730K would be used to measure the temperature of a small AC motor suspected
of overheating. The motor measures approximately 1 ft x 1 ft, so it has an area of 1 ft
2
.
If the OS730K is used to make the measurement from 60 ft. away, the reading will
have a large error. At this distance, the target area is 2 ft
2
. Therefore, the OS730K will
measure not just the temperature of the motor, but also the temperature of the physical
surroundings in its field of view, and average the two readings.
How inaccurate would the measurement be? If the motor’s operating temperature is
200°F and the background temperature is 75°F, and the motor’s area is half the target
area at the measurement distance, the following equation gives the average
temperature of the target area:
Tavg = ( Tbackground) ÷ 2
Solving for Tavg, we get (200 + 75) ÷ 2 or 137.5°F., which is what the OS730K would
display. In other words, trying to measure the temperature of the motor from 60 ft.
away introduced an error of (200-137.5) ÷ 200, or 31% into the measurement. In this
case, the measured temperature was 31% below the motor’s actual temperature
because the background is cooler than the motor.
To eliminate measurement error, the IRT must be moved close enough so the motor is
the only object in the target area (see figure below). For a motor with an area of 1 ft
2
and using an IRT with a D:S ratio of 30:1, the optimum measurement distance would
be 30 ft.
For best results, the targeted area (spot) should fall within the target’s boundaries, as in
the figure below.
Measuring a motor’s temperature
from the wrong (top) and right (bottom) distance
14
wall


















