GOLDBERG AND MÄKIVIRTA
AUTOMATED IN-SITU EQUALISATION
AES 23RD CONFERENCE, May 23-25, 2003
4
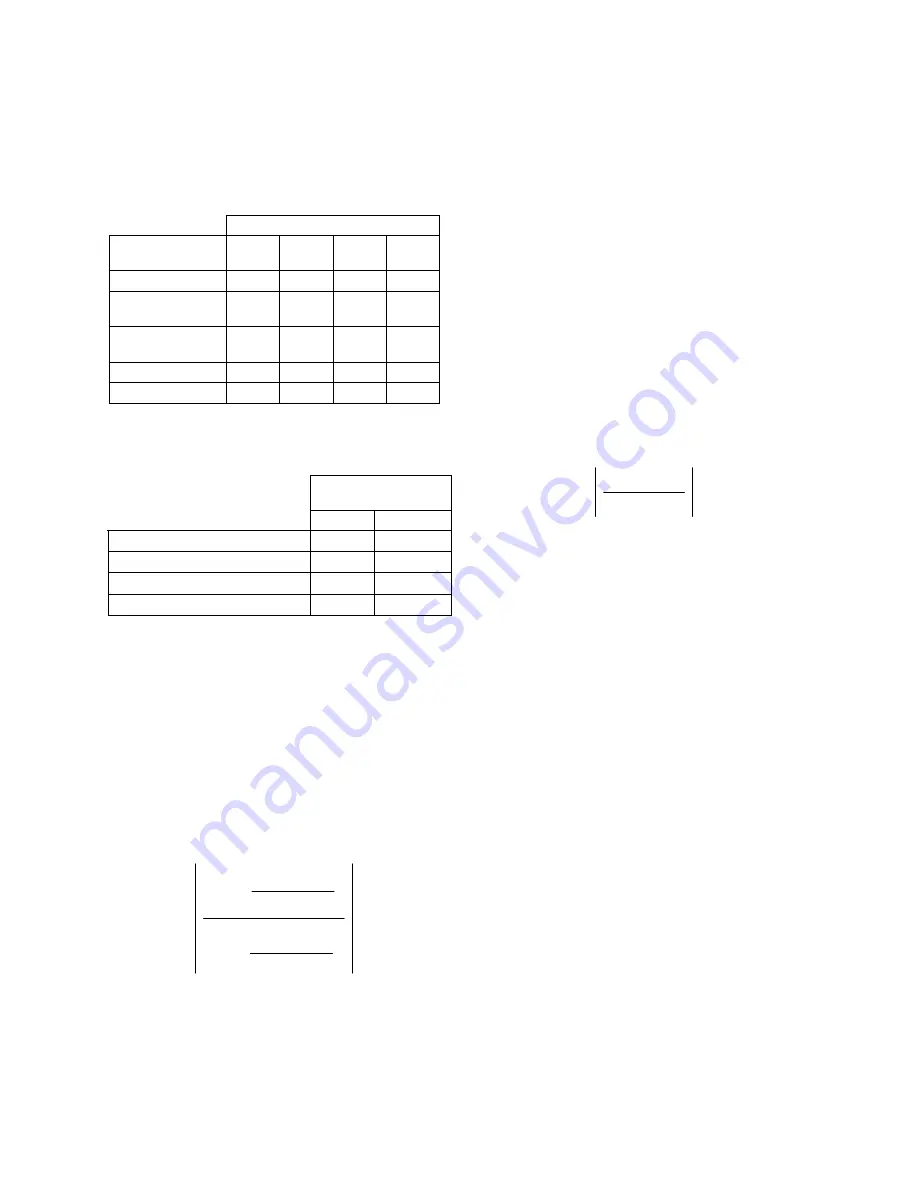
certain frequency ranges in each stage (Table 7).
Figure 5 in Appendix A shows a flow chart of the
software. A screenshot of the software graphic user
interface can be seen in Appendix B.
Table 6. Optimisation stages.
Type of loudspeaker
Optimisation
stage Large 3-way 2-way Small
2-way
Preset bass roll-off
9
9
9
9
Find midrange/
treble ratio
9
9
- -
Set bass tilt and
level
9
9
- -
Reset bass roll-off
9
9
9
9
Set treble tilt
9
-
9
9
Table 7. Optimiser frequency ranges;
f
HF
= 15 kHz;
f
LF
is the frequency of the lower –3 dB limit of the fre-
quency range.
Frequency Range
Limit
Low
High
Loudspeaker pass band
f
LF
f
HF
Midrange and treble driver band
500 Hz
f
HF
Bass roll-off region
f
LF
1.5
f
LF
Bass region
1.5
f
LF
6
f
LF
3.2.1. Pre-set Bass Roll-off
In this stage, the bass roll-off control is set to keep the
maximum level found in the ‘bass roll-off region’ as
close to the maximum level found in the ‘bass region’.
Once found the bass roll-off control is reset to one po-
sition higher, for example, –4 dB is changed to –2 dB.
The reason for this is to leave some very low bass en-
ergy for the bass tilt to filter. It is possible that the
bass tilt alone is sufficient to optimise the response
and less or no bass roll-off is eventually required. The
min-max type objective function to be minimised is
given by Equation 2,
[
]
[
]
3
2
2
1
0
0
,
,
,
,
)
(
)
(
)
(
max
)
(
)
(
)
(
max
min
f
f
f
f
f
f
f
x
f
x
f
a
f
x
f
x
f
a
E
b
a
m
b
f
m
f
m
a
=
=
=
(2)
where
x
(
f
) is the smoothed magnitude of the in-situ
frequency response of the system,
a
m
(
f
) is the bass
roll-off setting
m
currently being tested,
x
0
(
f
) is the
target response,
f
a
defines the ‘bass roll-off region’
(Table 7) and
f
b
defines the ‘bass region’ (Table 7).
User selected frequency ranges are not permitted.
The reason for this arrangement rather than using a
least squares type objective function is that the bass
roll-off tends to assume maximum attenuation to
minimise the RMS deviation. This type of objective
function does not yield the best setting, as subjectively
a loss of bass extension is perceived. This stage of the
optimiser algorithm takes six filtering steps (three for
small two-way models).
3.2.2. Midrange Level to Treble Level Ratio
The aim of this stage is to find the relative levels of
the midrange level and treble level controls required
to get closest to the target response. The least squares
type objective function to be minimised is given in
Equation 3,
df
f
x
f
x
f
a
E
f
f
f
m
m
2
0
2
1
)
(
)
(
)
(
min
∫
=
=
(3)
where
x
(
f
) is the smoothed magnitude of the in-situ
frequency response of the system,
a
m
(
f
) is the mid-
range and treble level control combination
m
currently
being tested,
x
0
(
f
) is the target response,
f
1
and
f
2
de-
fine the ‘midrange and treble driver band’
(Table 7).
The lower frequency bound is fixed at 500 Hz but a
user selectable high frequency value is permitted. The
default value is 15 kHz.
The midrange-to-treble level ratio is saved for per-
forming the third stage of the optimisation process.
The reason for this is to reduce the number of room
response control combinations to be tested in the next
stage. This stage of the optimisation algorithm takes
49 filtering steps and is not required for two-way
models or small two-way models.
3.2.3. Bass Tilt and Bass Level
This stage of the optimiser algorithm filters using all
possible combinations of bass tilt and bass level con-
trols for a given midrange/treble level difference. By
fixing this difference the total number of filter combi-
nations can be reduced substantially.
A constraint imposed in this stage is that only two of
the driver level controls can be set at any one time. If
three of the level controls are simultaneously set the
net effect is a loss of overall system sensitivity. Table
8 shows an example of incorrect and correct setting of
the driver level controls.



















