9 – Infrared Primer
A6700sc/A6750sc User’s Manual
50
Where:
W
λb
= Blackbody spectral radiant emittance at wavelength
λ.
c
= Velocity of light = 3 × 108 m/s
h
= Planck’s constant = 6.6 × 10-34 Joule sec.
k
= Boltzmann’s constant = 1.4 × 10-23 Joule/K.
T
= Absolute temperature (K) of a blackbody.
λ
= Wavelength (
μm).
Note
The factor 10-6 is used since spectral emittance in the curves is expressed in Watt/m2m. If the
factor is excluded, the dimension will be Watt/m2
μm.
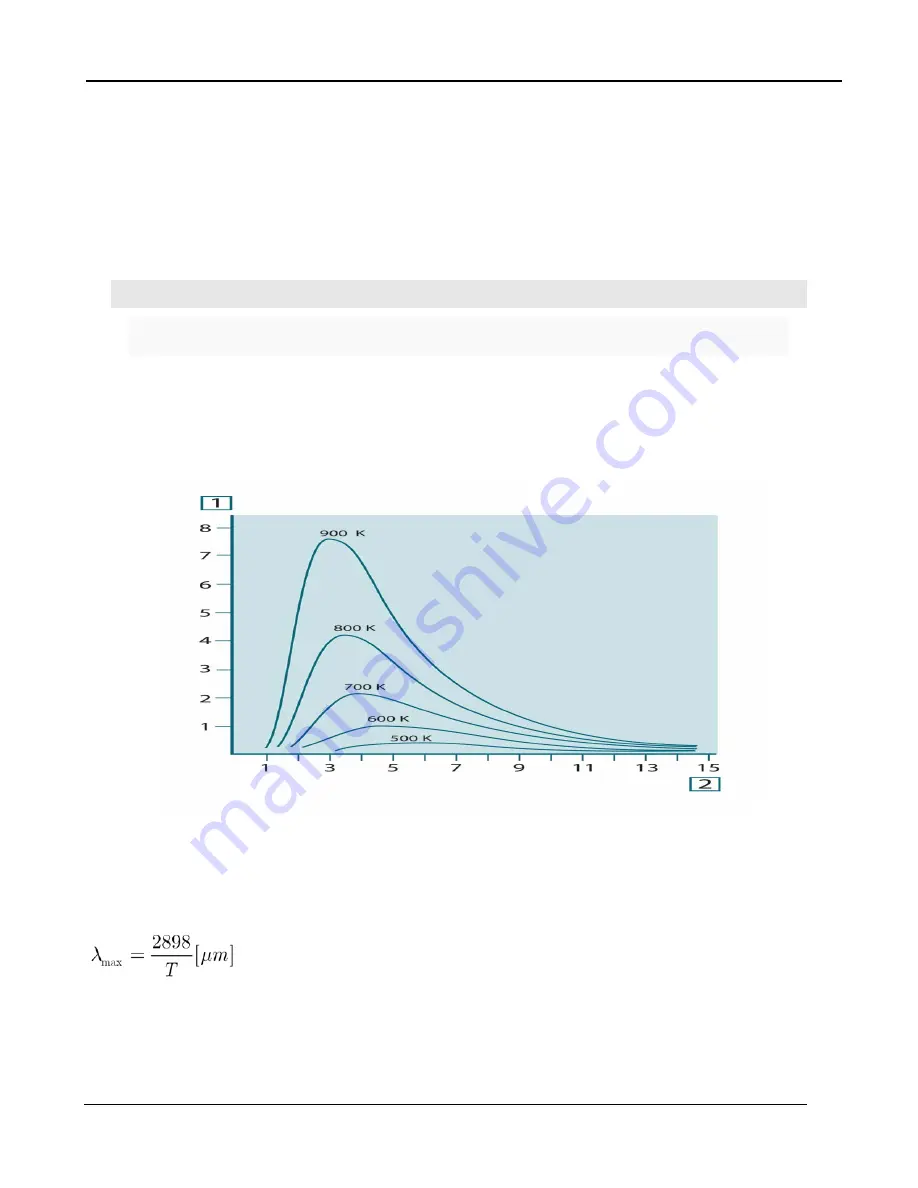
Planck’s formula, when plotted graphically for various temperatures, produces a family of curves.
Following any particular Planck curve, the spectral emittance is zero at
λ = 0, then increases rapidly to
a maximum at a wavelength
λmax and after passing it approaches zero again at very long
wavelengths. The higher the temperature, the shorter the wavelength at which maximum occurs.
Figure 8-8: Blackbody spectral radiant emittance according to Planck’s law, plotted for various
absolute temperatures. 1: Spectral radiant emittance (W/cm2 × 103(
μm)); 2: Wavelength (μm)
Wien’s Displacement Law
By differentiating Planck’s formula with respect to
λ, and finding the maximum, we have:
This is Wien’s formula (after Wilhelm Wien, 1864–1928), which expresses mathematically the
common observation that colors vary from red to orange or yellow as the temperature of a thermal
radiator increases. The wavelength of the color is the same as the wavelength calculated for
λmax. A
good approximation of the value of
λmax for a given blackbody temperature is obtained by applying






























