8
EN
SLC 420 IP 69 K
Operating instructions
Safety light curtain
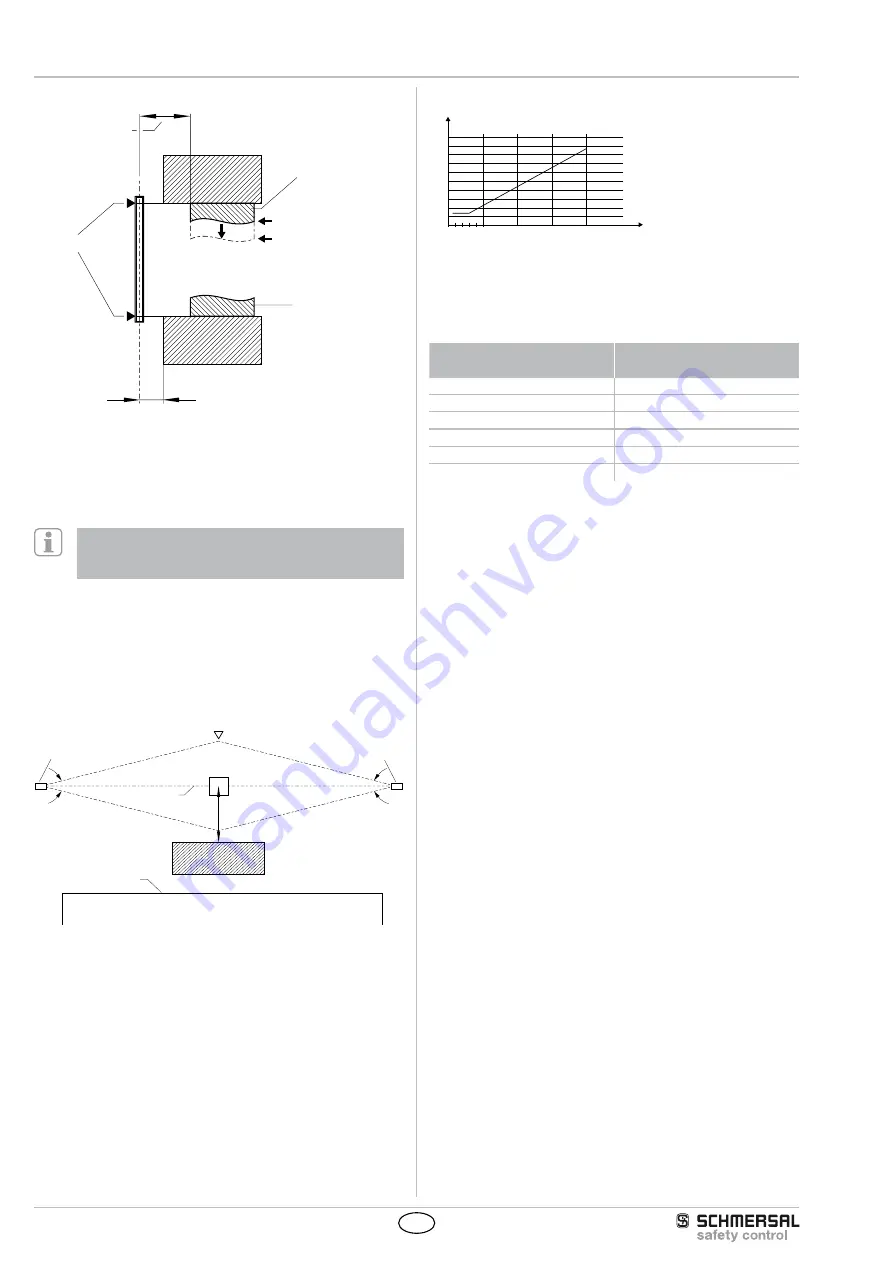
Safety distance to the hazardous area
Limit of the hazardous point
Safety distance (S)
Protection field marking
Tool - upper part
Signal to stop the
hazardous movement
Standstill of the hazardous
movement
t
n
= t
B
- t
A
Tool - lower part
t
A
S
t
B
≤
75 mm = max distance for protection against stepping over
To prevent persons from stepping over the protection field
this dimension must be imperatively respected and observed
The formulae and calculation examples are related to the vertical set-up
(refer to drawing) of the light curtain with regard to the hazardous point
Please observe the applicable harmonised EN standards and possible
applicable national regulations
The successor standards of the EN 999 for calculating the
minimum distances of the safety guards with regard to the
hazardous point are EN ISO 13855 and EN ISO 13857
3.4.1 Minimum distance to reflecting surfaces
During the installation, the effects of reflecting surfaces must be taken
into account In case of an incorrect installation, interruptions of the
protection field could possibly not be detected, which could lead to
serious injuries The hereafter-specified minimum distances with regard
to reflecting surfaces (metal walls, floors, ceilings or parts) must be
imperatively observed
8°
8°
a= 262 mm
Access direction
Receiver
Obstacle
optical axis
Transmitter
reflecting body
(eg Material container)
Limit of the hazardous
point
a=130mm
5°
5°
Safety distance a
a [mm]
D [m]
0
3 5
10
100
200
300
400
500
600
700
800
900
1000
15
20
Calculate the minimum distance to reflecting surfaces as a function of
the distance with an aperture angles of ± 25° degrees or use the value
from the table below
Distance between transmitter
and receiver [m]
Minimum distance a [mm]
02 … 30
130
4
175
5
220
7
310
10
440
15
660
Formula: a = tan 2.5° x L [mm]
a = Minimum distance to reflecting surfaces
L = Distance between transmitter and receiver
















