TM_s-MEXT_ME28relC_00_12_19_EN
Technical manual
TRANSLATION OF THE ORIGINAL INSTRUCTIONS
124
Parameter
(Decreases)
Constant
(Increases)
Promptness of
response
Overshoot
Balancing time
Error at full power
Stability
T
i
K
i
Increases
Increases
Increases
Cancels out
Worsens
The integral action can be disabled by setting the integral time to 0.
21.1.3
Derivative Action
The derivative action sets a control action based on the prediction of what will happen in the future. The value of this action is proportional to the error trend (increase or
decrease).
This action helps to improve dynamic performance, while maintaining the high value of the proportional action, but is less simple to adjust. It is useful in that, if the output
deviates too quickly from the setpoint value, the error derivative and, therefore, the derivative action, can be significant.
This action is defined using the derivative constant K
d
(also known as derivative gain) calculated with this formula:
𝐾
𝑑
= 𝐾
𝑝
∗ 𝑇
𝑑
Where T
d
is the value of the derivative time defined by one of the following parameters:
•
P20.07 (for the adjustment of direct expansion units with inverter compressor)
•
P20.23 (for humidifier adjustment)
•
P20.96 (for the adjustment of direct expansion units with compressors with delivery air adjustment active and Free Cooling).
The T
d
time defines the projected time horizon: If too small, it will not have a good anticipatory effect; if too large, its forecast may be completely wide of the mark.
The following table shows the reactions on the system caused by the
increase
of the derivative time and resulting increase of the derivative constant.
Parameter
(Increases)
Constant
(Increases)
Promptness of
response
Overshoot
Balancing time
Error at full power
Stability
T
d
K
d
Increases (slightly)
Decreases
Decreases (slightly)
Does not change
Improves
The derivative action can be disabled by setting the derivative time to 0.
21.1.4
The combined effect of the three actions
The control action of the system is, therefore, calculated, one moment at a time, as the sum of the three contributions (Proportional, Integral and Derivative).
The
P
roportional Action represents the
component most sensitive to the current value of the error
:
•
High K
p
values entail a significant reaction also for slight error variations.
•
Reduced values transfer on the control variable limited variations also in case of significant errors.
The
I
ntegral action varies in a linear manner following the action of proportionality coefficient K
p
/T
i
and, as mentioned above,
takes the past trend of the error into account
:
•
Reduced T
i
values lend greater importance to past system history.
•
High values decrease the weight of the integral action by transferring to the control variable variations that are more dependent on the current error value.
The
D
erivative action varies in a linear manner with the error derivative following the action of proportionality coefficient K
p
*T
d
and, as mentioned before,
takes the current
trend of the error into account
:
•
High T
d
values place greater importance on what may be the future trend of the error, with greater reliance on the algorithm
•
Lower values transfer to the control variable variations that are less dependent on future trends.
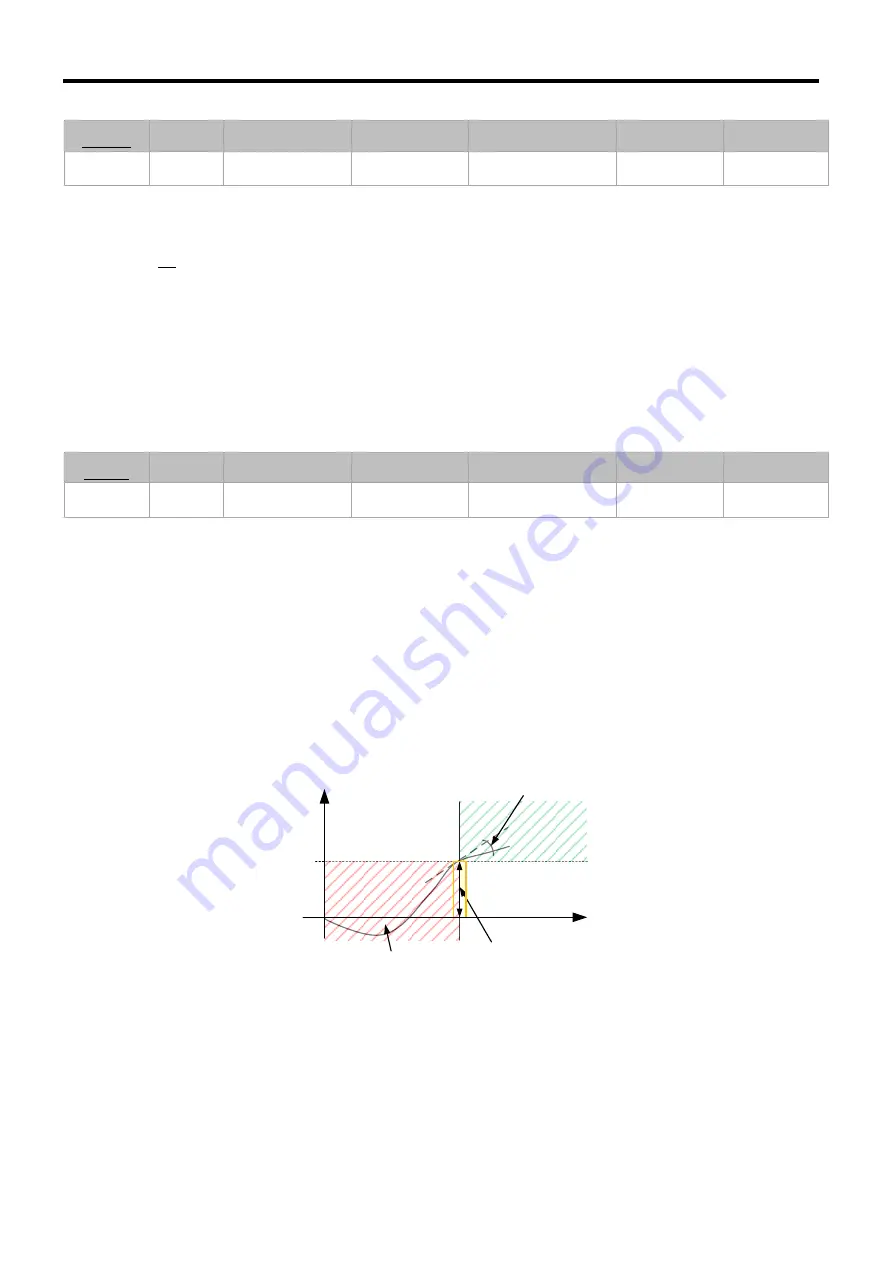
The image below illustrates what has been said above.
Error
Time
Present
K
p
Past
K
i
Future
K
d
Figure 21-2:
DIP control contribution relation chart
21.1.5
Anti-Windup control (control of integral error)
The PID adjuster has an integral error control function called Anti-Windup.
This function is used when the demand of the PID reaches 100%. In this case, without the function, the integral action of the controller would continue to integrate the error
and render the PID adjuster inactive even if the error were to decrease in relation to the setpoint, causing the system to overshoot. This would continue until the end of the
integral period (time T
i
).
This function stops the calculation of the integral action until demand falls again below 100%.





































