YOKOGAWA WT1800 User Manual Download Page 17 | Manualshive

Page: 17 / 167

background image

2-4

IM WT1801-01EN

Efficiency Equation (

η Formula)

You can create an efficiency equation by combining measurement function symbols. The WT1800 can determine
the energy conversion efficiency of the device using the numeric values of the measurement functions.

η1 to η4

You can create four efficiency equations (η1 to η4), using the following measurement functions as operands.

• The active powers of each element (P1 to P6)

• The active powers of the Σ functions (PΣA to PΣC)
• The motor output (Pm; on models with the motor evaluation option)

• Udef1 and Udef2

Udef1 and Udef2

To add active powers and motor output and use them in η1 to η4, use Udef1 and Udef2. You can add up to four

operands consisting of the measurement functions listed above.

Equation Examples
• Efficiency of a Single-Phase, Two-Wire Input/Single-Phase, Two-Wire Output Device

  Input: Power of element 1 (P1)
  Output: Power of element 2 (P2)
  Efficiency equation: P2/P1 × 100 (%)

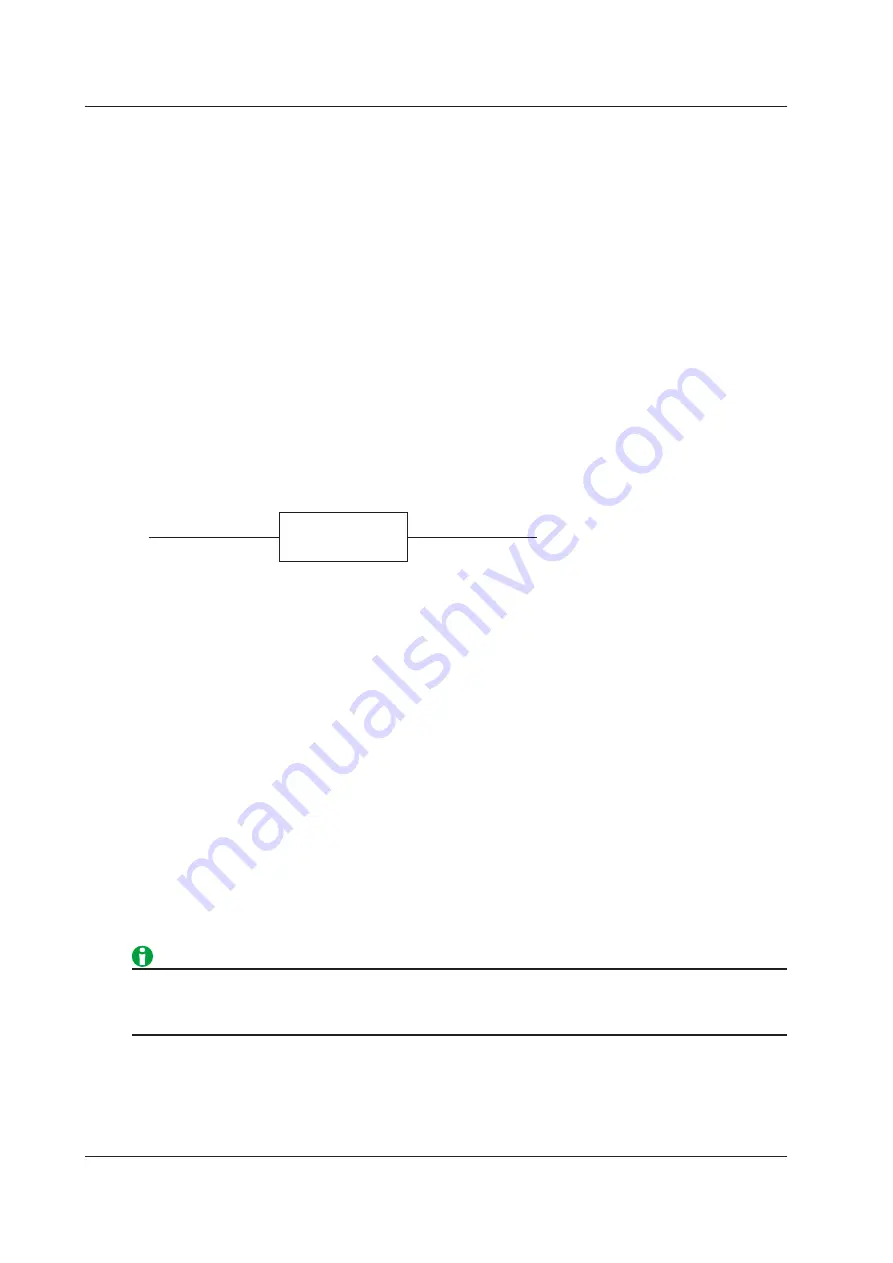
Converter

(inverter, etc.)

Input power: P1

Output power: P2

• Efficiency of a Single-Phase, Two-Wire Input/Three-Phase, Three-Wire Output Device

Input: Power of element 1 (P1)

Output: Σ power of elements 2 and 3 (PΣA)
Efficiency equation: PΣA/P1 × 100 (%)

• Efficiency of a Three-Phase, Three-Wire Input/Three-Phase, Three-Wire Output Device

  Input: Σ power of elements 1 and 2 (PΣA)
  Output: Σ power of elements 3 and 4 (PΣB)
  Efficiency equation: PΣB/PΣA × 100 (%)

• Efficiency of a Motor with a Single-Phase, Two-Wire Input

  Input: Power of element 1 (P1)
  Output: Motor output (Pm)
  Efficiency equation: Pm/P1 × 100 (%)

• Efficiency of a Motor with a Three-Phase, Three-Wire Input

Input: Σ power of elements 1 and 2 (PΣA)

Output: Motor output (Pm)

Efficiency equation: Pm/PΣA × 100 (%)

To correctly compute the efficiency, set the power coefficients of all elements so that all power units used in

the computation are the same. For example, the efficiency cannot be computed correctly if elements or wiring
units used in the computation have different power units, such as W (watt) and J (joule).

2 Fundamental Measurement Conditions

«
...
15
16
17
18
19
...
»

Summary of Contents for WT1800

Page 1: ...IM WT1801 01EN 2nd Edition Precision Power Analyzer WT1800 Features Guide ...

Page 2: ...s on how to use them Notes The contents of this manual are subject to change without prior notice as a result of continuing improvements to the instrument s performance and functionality The figures given in this manual may differ from those that actually appear on your screen Every effort has been made in the preparation of this manual to ensure the accuracy of its contents However should you hav...

Page 3: ... ALL 2 9 Voltage Range RANGE UP DOWN V 2 9 Auto Voltage Range AUTO V 2 10 Current Range RANGE UP DOWN A 2 11 Auto Current Range AUTO A 2 11 Power Range 2 12 External Current Sensor Range EXT SENSOR option 2 12 External Current Sensor Conversion Ratio SENSOR RATIO option 2 13 External Current Sensor Range Display Format DIRECT MEASURE option 2 14 Scaling SCALING 2 14 Valid Measurement Range CONFIG ...

Page 4: ... Auxiliary Input Conditions MOTOR AUX SET 5 1 Input Signal Name Aux Name 5 1 Scaling Factor Scaling 5 1 Unit Unit 5 1 Analog Input Range 5 1 Linear Scaling of Analog Input 5 2 Line Filter Line Filter 5 3 6 Holding Measured Values and Performing Single Measurements Holding Measured Values HOLD 6 1 Single Measurement SINGLE 6 1 7 Numeric Data Display Numeric Data Display NUMERIC 7 1 Display Format F...

Page 5: ...ping and Resetting Integration Start Stop Reset 9 5 Integration Conditions Integ Set 9 7 Integration Mode Mode 9 7 Integration Timer Integ Timer 9 10 Scheduled Times for Real Time Integration Real time Control 9 10 Integration Auto Calibration On Off Auto Cal 9 11 Watt Hour Integration Method for Each Polarity WP Type 9 11 Current Mode for Current Integration q Mode 9 11 Rated Time of Integrated D...

Page 6: ...ing Cursor Movement Linkage 15 2 Measured Items 15 2 Cursor Movement 15 4 16 High Speed Data Capturing High Speed Data Capturing OTHERS High Speed Data Capturing 16 1 High Speed Data Capturing HS Settings FORM 16 4 Number of Data Captures Capture Count 16 4 Viewing and Optimizing the Maximum Capturing Count Optimize Count 16 4 Capture Control Settings Control Settings 16 5 Recording to a File Reco...

Page 7: ...int ON 20 2 Automatic Printing Auto Print Settings 20 2 Comment Comment 20 3 Paper Feed Paper Feed 20 3 Print Timing for Different Print Modes 20 4 Printing PRINT 20 6 21 Ethernet Communication Network TCP IP TCP IP 21 2 FTP Server FTP Server 21 3 Network Drive Net Drive 21 4 SNTP SNTP 21 5 22 Utility Utility UTILITY 22 1 Overview System Overview 22 2 Initializing the Settings Initialize Settings ...

Page 8: ...e voltage average Yes Yes Urmn Rectified mean voltage Yes Yes Uac AC voltage component Yes Yes U pk Maximum voltage Yes No U pk Minimum voltage Yes No CfU Voltage crest factor Yes No Current Function Description Input Element Wiring Unit Irms True rms current Yes Yes Imn Rectified mean current calibrated to the rms value Yes Yes Idc Simple current average Yes Yes Irmn Rectified mean current Yes Ye...

Page 9: ...P values Yes Yes q Sum of positive and negative ampere hours Yes Yes q Sum of positive I values Yes Yes q Sum of negative I values Yes Yes WS Volt ampere hours Yes Yes WQ Var hours Yes Yes Efficiency Function Description η1 to η4 Efficiency User Defined Functions Function Description F1 to F20 User defined functions User defined events Function Description Ev1 to Ev8 User defined events 1 Items Th...

Page 10: ... Uthf Telephone harmonic factor of the voltage Yes No Ithf Telephone harmonic factor of the current Yes No Utif Telephone influence factor of the voltage Yes No Itif Telephone influence factor of the current Yes No hvf Harmonic voltage factor Yes No hcf Harmonic current factor Yes No K factor K factor Yes No ΦUi Uj1 Phase difference between the fundamental voltage of element i Ui 1 and the fundame...

Page 11: ... Utif Yes No No No Itif Yes No No No hvf Yes No No No hcf Yes No No No K factor Yes No No No Functions with parentheses will produce different values depending on which of the following is contained in their parentheses Total Total value The total value of all harmonic components from the minimum order to N For information about how the value is determined see appendix 1 in the getting started gui...

Page 12: ...ion Description Speed Motor rotating speed Torque Motor torque SyncSp Synchronous speed Slip Slip Pm Mechanical output of the motor mechanical power EaU1 to 6 Electrical angle Phase angles of U1 to I6 with the falling edge of the signal received through the Z terminal of the motor evaluation function as the reference EaI1 to 6 On models with the harmonic measurement option or the simultaneous dual...

Page 13: ...ower of various single phase and three phase power transmission systems single phase two wire single phase three wire three phase three wire three phase four wire and three phase three wire with three voltage three current method Wiring Unit The wiring unit is a set of two or three input elements of the same wiring system that are grouped to measure three phase power There can be up to three wirin...

Page 14: ...e are multiple wiring units element numbers are assigned to them in ascending order The element numbers are assigned to ΣA ΣB and then ΣC Wiring units are composed of input elements that are next to each other Wiring units cannot consist of input elements that are not next to each other A wiring unit must either be composed of only 50 A input elements or only 5 A input elements Wiring units cannot...

Page 15: ...m to match the actual wiring of the circuit under measurement The method in which the Σ functions wiring unit measurement functions are determined varies depending on the wiring system If the selected wiring system does not match the wiring of the actual circuit measurements and computation will not be correct Wiring System Display The wiring system configuration is displayed on the right side of ...

Page 16: ...off settings are changed to match the setting of the input element whose measurement range is highest If multiple input elements are set to a common highest measurement range the setting of the input element with the smallest input element number takes precedence In the valid measurement range settings all measurement ranges are enabled selected The synchronization source for a wiring unit is set ...

Page 17: ...fficiency equation P2 P1 100 Converter inverter etc Input power P1 Output power P2 Efficiency of a Single Phase Two Wire Input Three Phase Three Wire Output Device Input Power of element 1 P1 Output Σ power of elements 2 and 3 PΣA Efficiency equation PΣA P1 100 Efficiency of a Three Phase Three Wire Input Three Phase Three Wire Output Device Input Σ power of elements 1 and 2 PΣA Output Σ power of ...

Page 18: ... option Settings That Can Be Configured Independently Even When Independent Input Element Configuration Is Turned Off External current sensor conversion ratio option Scaling values VT ratio CT ratio and power coefficient Input filters line filter and frequency filter These settings can be configured independently for each input element regardless of whether independent input element configuration ...

Page 19: ... between two elements can be computed on a single phase three wire system or on a three phase three wire system When you perform delta computation on wiring unit ΣA the available measurement functions are as follows ΔU1rms UdiffA ΔU1mn UdiffA ΔU1dc UdiffA ΔU1rmn UdiffA ΔU1ac UdiffA ΔIrms IdiffA ΔImn IdiffA ΔIdc IdiffA ΔIrmn IdiffA ΔIac IdiffA In the measurement functions rms mn mean dc rmn r mean ...

Page 20: ...star transformation Delta Star Using the data from a three phase three wire system that uses a three voltage three current method you can compute the data of a star connection from the data of a delta connection This function is useful when you wish to observe the phase voltage of an object that has no neutral line such as a motor The center N of the star connection is computed as the center of th...

Page 21: ...utions of the sampled data to be different This results in errors The numbers 1 2 and 3 that are attached to delta computation measurement function symbols have no relation to the element numbers The computation of all delta measurement functions from ΔU1 to ΔPΣ varies depending on the wiring system and the delta computation type For details see appendix 1 in the getting started guide IM WT1801 03...

Page 22: ...elect from 1 5 V 3 V 6 V 10 V 15 V 30 V 60 V 100 V 150 V 300 V 600 V and 1000 V When the Crest Factor Is Set to CF6 You can select from 0 75 V 1 5 V 3 V 5 V 7 5 V 15 V 30 V 50 V 75 V 150 V 300 V and 500 V Auto Range Click here Set the range in reference to the rms value of the input signal For example if you are applying a 100 Vrms sinusoidal signal set the range to 100 V When measuring a signal o...

Page 23: ...ed on all input elements in the wiring unit when any of the elements in the unit meets the range increase conditions described above Range Decrease The measurement range is decreased when all the following conditions are met The data of Urms or Irms is less than or equal to 30 of the measurement range The data of Urms or Irms is less than or equal to 105 of the next lower range The crest factor is...

Page 24: ...25 mA 50 mA 100 mA 250 mA 500 mA 1 A and 2 5 A For 50 A Input Elements When the Crest Factor Is Set to CF3 You can select from 1 A 2 A 5 A 10 A 20 A and 50 A When the Crest Factor Is Set to CF6 You can select from 500 mA 1 A 2 5 A 5 A 10 A and 25 A Auto Range This is the same as the auto range feature for voltage Click here When the secondary output of a CT current transformer or a clamp type curr...

Page 25: ... IM WT1801 03EN In auto range mode because the voltage and current ranges switch independently according to range increase and decrease conditions different power ranges may be set for the same power value External Current Sensor Range EXT SENSOR option The output of current sensors that produce voltage such as shunts and clamps can be applied to an element s external current sensor input connecto...

Page 26: ...nt Sensor Conversion Ratio Exec Copy Σ Copy the external current sensor conversion ratio of the selected input element to the other input elements in the same wiring unit External Current Sensor Range and Conversion Ratio Configuration Example When you measure a current with a maximum value of 100 A using a current sensor that produces 10 mV when 1 A of current is flowing the maximum voltage that ...

Page 27: ...e SCALING key and the Scaling indicator at the top of the screen illuminate Applicable Measurement Functions Voltage U current I power P S and Q maximum and minimum voltages U pk and U pk and maximum and minimum currents I pk and I pk ON The measurement functions above are multiplied by the VT ratio CT ratio or power coefficient OFF The measurement functions above are not multiplied by the VT rati...

Page 28: ...ollowing range 0 0001 to 99999 9999 Copying the Power Coefficient Exec Copy Σ Copy the power coefficient of the selected input element to the other input elements in the same wiring unit If the value of the result of multiplying the measured value by the VT ratio CT ratio or power coefficient scaling factor exceeds 9999 99 M OF will appear in the numeric data display frame You can view the VT and ...

Page 29: ...urs when this feature is disabled the WT1800 increases the measurement range switching between valid measurement ranges measurement ranges whose check boxes have been selected You can specify valid current measurement ranges for each input element type 50A Input Element Select the valid direct input measurement ranges of 50 A input elements 5A Input Element Select the valid direct input measuremen...

Page 30: ...ter measurement range For example even if CF is set to 3 measurement is possible for signals with a crest factor greater than or equal to 5 when the measured value rms value is less than 60 of the measurement range If the minimum effective input 1 of the measurement range is being applied when CF is set to 3 measurement for CF 300 is possible The voltage range current range effective input range a...

Page 31: ... update interval For details see appendix 5 in the getting started guide IM WT1801 03EN Measurement Period for Measurement Functions Used in Harmonic Measurement The measurement period extends from the first sample in the data update interval for the number of points indicated below When the data update interval is 50 ms 100 ms or 200 ms 1024 points When the data update interval is 500 ms 1 s 2 s ...

Page 32: ...ndicator at the top of the screen illuminate Selecting OFF disables the line filter Copying the Line Filter Setting Exec Copy Σ Copy the line filter on off setting and cutoff frequency of the selected input element to the other input elements in the same wiring unit Line Filter for High Speed Data Capturing Click here Frequency Filter FREQ FILTER The frequency filter is inserted into the frequency...

Page 33: ... longer than the data update interval The lowest measurable AC signal frequency varies depending on the data update interval The measured value may not be stable if an AC signal of a frequency lower than the low frequency measurement limit see section 6 5 in the getting started guide IM WT1801 03EN is measured Averaging AVG You can take exponential or moving averages of the numeric data The averag...

Page 34: ... is Lin moving average set the average count to a value within the following range 8 to 64 Measurement Functions That Are Averaged The measurement functions that are directly averaged are indicated below Other functions that use these functions in their computation are also affected by averaging For details about how the values of the measurement functions are determined see appendix 1 in the gett...

Page 35: ... less responsive measured values Displaying the Setup Parameter List INPUT INFO The setup parameter list appears in the top half of the screen Display Format FORM Input Element Settings List Power Element Settings The wiring system measurement range scaling factor synchronization source line filter and frequency filter settings for each element are displayed Measurement Range Settings List Range S...

Page 36: ...items appear Input element group Element Settings PLL source of group Hrm1 Hrm1 PLL Source Measured harmonic orders of group Hrm1 Min Order Max Order Distortion factor equation of group Hrm1 Thd Formula PLL source of group Hrm2 Hrm2 PLL Source Measured harmonic orders of group Hrm2 Min Order Max Order Distortion factor equation of group Hrm2 Thd Formula PLL Source PLL Source For harmonics to be me...

Page 37: ...easured values are displayed four data updates after the change Correct measured values may not be obtained immediately after the PLL source or its frequency changes because the PLL circuit inside the WT1800 redetects the frequency Measured Harmonic Orders Min Order Max Order The harmonic measurement range can be specified The harmonic orders specified here are used to determine the numeric data o...

Page 38: ... different frequencies You can measure the input and output harmonics of an AC AC converter whose input and output frequencies are different This setting does not appear on models with the harmonic measurement option Element1 to Element6 Use the soft keys to select an element and then assign the element to group Hrm1 or group Hrm2 Input elements that are assigned to the same wiring unit are assign...

Page 39: ... irrelevant to the harmonic measurement For example when an input signal with a fundamental frequency of 50 Hz is measured up to the 50th order the frequency of the 50th order is 2 5 kHz Thus a 5 kHz anti aliasing filter is used to eliminate high frequency components that are greater than or equal to approximately 5 kHz which are irrelevant to harmonic measurement The WT1800 uses the line filter a...

Page 40: ... That This Instrument Can Measure Click here Models with the Auxiliary Input Option The Aux Settings dialog box appears Click here Motor Evaluation Settings You can configure the following motor evaluation settings Scaling factor Scaling Unit Unit Input signal type Sense Type Analog input range Linear scaling of analog input Line Filter Line Filter Synchronization Source Sync Source Pulse input ra...

Page 41: ...at the unit of Pm is W 2π 60 Motor output Pm Speed Torque S Speed The rotating speed determined from the number of pulses per revolution Torque The torque determined from the torque signal pulse rating S The scaling factor Unit Unit Number of characters Up to eight Usable characters Spaces and all characters that are displayed on the keyboard Input Signal Type Sense Type You can select which of th...

Page 42: ...r torque signal falls below 30 of the measurement range and the peak value of the input signal is less than 125 of the lower range When non periodic pulse waveforms are applied during auto range the range may not remain constant If this happens use the fixed range setting Fixed Range Analog Range You can select one of the following input ranges 20 V 10 V 5 V 2 V or 1 V Linear Scaling of Analog Inp...

Page 43: ...ill be offset Reset the NULL value Computing the Input Signal Slope and Offset by Specifying Two Points Calculation On the input characteristic graphs of the rotating speed and torque you can specify two measured rpm or N m values Point1Y and Point2Y in relation to two input voltage values Point1X and Point2X Measured values Point1X and Point2X 1 000 T to 1 000 T Computed values Point1Y and Point2...

Page 44: ...ce for motor efficiency measurement to the same sync source that is set in the fundamental measurement conditions This ensures that the measurement period is in sync with the measurement functions such as those for voltage current and active power Pulse Input Range Set an appropriate range for the maximum and minimum input signal values For example when you are measuring signals for rotating speed...

Page 45: ...ow configure the pulse input range and pulse rating settings as indicated below Upper limit of the pulse input range Pulse Range Upper 20 0000 Lower limit of the pulse input range Pulse Range Lower 20 0000 Positive rated torque signal value Rated Upper 50 0000 Negative rated torque signal value Rated Lower 50 0000 Positive rated torque signal pulse frequency Rated Freq Upper 15000 Negative rated t...

Page 46: ...ng Synchronous Speed Sync Speed Motor Poles Pole Set the number of motor poles to a value from 1 to 99 This number is used to compute the sync speed Frequency Measurement Source Source Select the frequency measurement source to use to compute the sync speed from the options below The frequency measurement source is used to compute the sync speed The available options vary depending on the installe...

Page 47: ...asure electrical angles Electrical Angle Correction Electrical Angle Correction Set the electrical angle correction value Correction Value Correction Value Set the correction value to a number from 180 00 to 180 00 Clearing the Correction Value Clear Correction Set the correction value to 0 00 Automatically Computing the Correction Value Auto Enter Correction The WT1800 automatically sets the corr...

Page 48: ...ut Pm Motor power consumption PΣA When the Converter and Motor Inputs Are Wired to ΣA and ΣB Respectively 100 Motor output Pm W PΣB W Motor efficiency 100 Motor output Pm W PΣA W Total efficiency Converter inverter etc Motor Motor output Pm PΣB PΣA Motor power consumption Motor and converter power consumption When the Converter and Motor Inputs Are Wired to ΣB and ΣA Respectively 100 Motor output ...

Page 49: ...the input signal name Aux Name setting Click here Analog Input Range Set the auxiliary input analog input range Turning Auto Range On and Off Analog Auto Range Select whether to turn auto range on or off When auto range is on the WT1800 automatically switches between the following ranges according to the size of the auxiliary input 20 V 10 V 5 V 2 V 1 V 500 mV 200 mV 100 mV and 50 mV Range Increas...

Page 50: ...per 1 V When There Is Offset in the Auxiliary Input Voltage If you set S to 1 the scaling factor does not affect the computation and the previous equation becomes Auxiliary input measured value AX B NULL You can scale the auxiliary input by setting the offset value B and setting the auxiliary input slope A to the number of units per 1 V If you enable the NULL function and then change the auxiliary...

Page 51: ...frequency noise by inserting a line filter into the circuit used to measure the Aux1 and Aux2 auxiliary inputs You can select the cutoff frequency from the following options OFF 100 Hz and 1 kHz Selecting OFF disables the filter 5 Auxiliary Input Conditions Option ...

Page 52: ...ing integration see the sections on holding and releasing integration Click here Single Measurement SINGLE While the display is held the signal is measured once at the data update interval and then the display is re held If you press SINGLE when the display is not held measurement restarts from that point Using an External Signal to Hold Measured Values and Perform Single Measurements Option On mo...

Page 53: ...t You can select the number of numeric data items that are displayed simultaneously from the choices below or choose to display a list of items 4 Value Display 4 Items Four numeric data values are displayed in one column 8 Value Display 8 Items When the display mode is Numeric eight numeric data values are displayed in one column When the display is split eight numeric data values are displayed in...

Page 54: ...r P Uhdf Ihdf or Phdf is displayed Harmonic order data display area Dual Harmonics List Display Hrm List Dual option When the display mode is Numeric the numeric values of two measurement functions are displayed in two separate columns each containing up to 22 numeric values When the display is split the numeric values of two measurement function are displayed in two separate columns each containi...

Page 55: ... PAGE The previous page is displayed In the 4 8 and 16 Value Displays You can switch between and display pages 1 to 12 In the Matrix Display You can switch between and display pages 1 to 9 In the All Items Display The first page is always displayed in the top half of the screen You can switch between pages 2 and later pages in the bottom half of the screen When the display is split and the All Ite...

Page 56: ... ITEM The display item options vary depending on the current display Numeric data display format 4 8 and 16 value displays 4 Items 8 Items 16Items Matrix display Matrix All Items display All Items Single Harmonics and Dual Harmonics Lists Hrm List Single Dual option Custom display Custom Waveform display items Trend display items Bar graph display items Vector display items High speed data capturi...

Page 57: ...ction 6 6 in the getting started guide IM WT1801 03EN and the data measurement interval will be 100 ms In this case the time required for harmonic measurement is approximately 150 ms or greater data measurement interval data processing time To measure and display harmonic data set the data update interval to a value greater than or equal to 200 ms There is no overload value indication OL or zero i...

Page 58: ...t can be specified vary depending on the measurement function For details see Harmonic Measurement Function Orders Click here The numeric data corresponding to harmonic orders above the maximum measurable harmonic order is displayed as no data For information about the maximum measurable harmonic order see Maximum Harmonic Order to Be Measured Max Order Click here Resetting the Display Items Reset...

Page 59: ...umn Settings Number of Columns Column Num You can set the number of columns to 4 or 6 Column Number Column No Select the number of the column that you want to configure Element Element Σ You can select the element wiring unit from the options below The available options vary depending on the installed elements None Element1 Element2 Element3 Element4 Element5 Element6 ΣA ΣB and ΣC If you select No...

Page 60: ...tting the order in the 4 8 and 16 value displays Click here Turning the Display of the Numeric Data for All Elements and Wiring Units On and Off Display All Elements OFF The numeric data is displayed in six columns If there is a total of seven or more elements and wiring units you can change the displayed elements and wiring units by pressing the left and right cursor keys ON When there is a total...

Page 61: ... in the harmonic order data display area This is the same as direct function selection in the 4 8 and 16 value displays However when you are displaying the single harmonics or dual harmonics list you can only select measurement functions that have harmonic order data You can press U I P to select U I or P You can press S Q λ Φ to select S Q λ Φ ΦU or ΦI WP q TIME FU FI η and U I MODE are invalid E...

Page 62: ...ge After you properly load a display configuration file and a background file if you restart the WT1800 and the same background file is not in the same location the background will return to its default Simultaneously Loading a Display Configuration File and a Background File Load Items Bmp When you select a display configuration file TXT from the file list and load it if there is a background fil...

Page 63: ...appears when you set Function to None Enter the character string to display in the numeric data box You can enter a string of up to 15 characters in length If you do not set Function to None instead of the String menu item the Order menu item appears X Display Position X Pos Set the position where the left edge of the numeric data box will appear on the screen to a value from 0 the left edge of th...

Page 64: ...erations Utility Click here Automatic File Naming Auto Naming This is the same as the auto naming feature for saving and loading data Click here File Name File Name This is the same as file name setting for saving and loading data Click here Saving Save Exec Saves the display configuration Note that if there is a file with the same name in the save destination it will be overwritten without warnin...

Page 65: ... by combining operands The measurement functions that you can specify for the efficiency equation are fixed at power and motor output However by using user defined functions you can create equations consisting of measurement functions other than power and motor output measurement functions to determine ratios other than efficiency Selecting Which User Defined Function to Configure Select the numbe...

Page 66: ... pk UPPK I pk IPPK Pc PC U pk UMPK I pk IMPK P pk PPPK CfU CFU CfI CFI P pk PMPK fU FU fI FI Integrated power Wp WH q AH Time TI Wp WHP q AHP WS SH Wp WHM q AHM WQ QH Efficiency η1 ETA1 to η4 ETA4 User defined functions F1 F1 to F20 F20 User defined events Ev1 EV1 to Ev8 EV8 Harmonic Measurement Option U k UK I k IK P k PK S k SK Q k QK λ k LAMBDAK ΦU k UPHI ΦI k IPHI Φ k PHIK Z k ZK Rs k RSK Xs k...

Page 67: ...nput Option Aux1 AUX1 Aux2 AUX2 Setting Operand Parameters The parameters that you need to enter depend on whether the function is followed by or Setting Parameters for Functions Followed by Specify the element to the left of the comma and specify the harmonic order to the right of the comma For example E1 OR2 Symbols used to represent elements E1 to E6 Elements 1 to 6 E7 to E9 Wiring units ΣA to ...

Page 68: ...ivided by F1 and set F5 as F4 divided by F1 However if you enter a user defined equation with a number that is greater than or equal to its own number correct results will not be obtained For example if you set user defined function F3 to F1 F3 or to F1 F4 the computed result will be displayed as no data or OF overflow Operators The following operators can be used in equations Operator Example Des...

Page 69: ...s whose maximum values will be held using a user defined function The different types of operands are listed below measurement function operand Urms URMSMAX Irms IRMSMAX P PMAX Umn UMEANMAX Imn IMEANMAX S SMAX Udc UDCMAX Idc IDCMAX Q QMAX Urmn URMEANMAX Irmn IRMEANMAX Uac UACMAX Iac IACMAX U pk UPPEAKMAX I pk IPPEAKMAX P pk PPPEAKMAX U pk UMPEAKMAX I pk IMPEAKMAX P pk PMPEAKMAX To hold the maximum...

Page 70: ...r specifying judgment conditions from the following options Range Range Specify judgment conditions using ranges of measurement function values or differences from a reference value Condition Condition Specify judgment conditions using user defined events Range Range Specify the judgment condition here when you have set the judgment condition specification method to Range Function Function You can...

Page 71: ...below When you reach the maximum number of combinable user defined events no AND OR END specification box appears to the right of the last event Ev1 0 You cannot use other user defined events as conditions Set the judgment condition using a range Ev2 1 Ev1 Ev3 2 Ev1 and Ev2 Ev4 3 Ev1 to Ev3 Ev5 4 Ev1 to Ev4 Ev6 5 Ev1 to Ev5 Ev7 6 Ev1 to Ev6 Ev8 7 Ev1 to Ev7 END Select END to end the definition of ...

Page 72: ...ned for the computation Because the equations for deriving the apparent and reactive power for distorted waveforms are not defined none of the equations can be said to be more correct than the other Therefore the WT1800 provides three equations Type 1 to Type 3 for determining the apparent power and reactive power Unlike apparent power and reactive power active power is derived directly from the s...

Page 73: ...1976 IEC76 1 1993 Equations for each applicable standard P P1 P2 Urms Umn 2 Pc P Umn Urms Umn 1 Pc IEC76 1 1976 IEC76 1 1993 Pc Corrected power P Active power Urms True rms voltage Umn Voltage s rectified mean calibrated to the rms value P1 P2 Coefficients specified by the applicable standard Coefficients P1 and P2 You can set coefficients P1 and P2 to values within the range of 0 0001 to 9 9999 T...

Page 74: ...ower factor λ is greater than 1 and less than or equal to 2 Φ returns 0 If λ is greater than 2 Φ returns an error Error is displayed On models with the harmonic measurement option the phase differences ΦU and ΦI of harmonic orders 1 to 500 of the voltage and current are always displayed using an angle between 0 and 180 no sign for lead and negative sign for lag Master Slave Synchronization Measure...

Page 75: ...e measured so there is no need to set which frequencies to measure Thus even if you press SHIFT MEASURE FREQ MEASURE the Freq Items menu will not appear If frequency measurements are unstable because of noise try using the frequency filter The period cannot be detected if the AC amplitude is small For information about detectable frequency levels see the conditions listed in Frequency Measurement ...

Page 76: ...ration In real time normal integration mode and real time continuous integration mode once the scheduled integration stop time is reached Stop appears in orange Even if you press Start integration is not resumed To start integration you must first reset it Ready In real time normal integration mode when you press Start before the scheduled integration start time is reached Ready and the scheduled ...

Page 77: ...egration is stopped and the integration time and integrated value are held The integration time reaches the maximum integration time 10000 hours The integrated value of WP q WS or WQ reaches the maximum or minimum displayable value given above Integration When the MAX Hold Feature Is Enabled The WT1800 determines and displays the integrated value by summing the value that is measured at every data...

Page 78: ...rt stop and reset integration For details about the remote control feature see appendix 4 6 in the getting started guide IM WT1801 03EN Backup When a Power Failure Occurs If a power failure occurs when integration is in progress the integration result is held When the power returns integration is stopped and the integration result calculated up to the point when the power failure occurred is displ...

Page 79: ... with wiring unit integration such as the integrated active power and apparent power functions return errors Independently Integrated Elements Element Object This setting is valid when independent integration is enabled You can select which elements to start stop and reset the integration of by selecting the elements check boxes All ON All elements are controlled All OFF No elements are controlled...

Page 80: ...ement range switches to a fixed range Stopping Integration Stop You can force integration to stop The integration time and integrated value are held When you force integration to stop the STOP indicator blinks and Stop appears in yellow as the integration status indication You can press Start to resume integration However after the automatic stopping of integration which is discussed later you can...

Page 81: ...g SINGLE to execute a single measurement The relationship between the hold function and the start and stop operations is as follows If you start integration while the display is held the display and communication output do not change When you release the hold function turn it off or make a single measurement by pressing SINGLE the integration result at that point is displayed and transmitted ON HO...

Page 82: ...ation Key operation Repeats when the timer expires Real time normal integration mode R Normal Date and time Date and time Real time continuous integration mode R Continuous Date and time Date and time Repeats when the timer expires Manual integration mode When you set the integration mode to normal integration mode Normal and set the integration timer to 00000 00 00 the WT1800 performs integration...

Page 83: ...time Integrated value Continuous Integration Mode Continuous integration Continuous You can set a relative integration time Integration starts when you press Start When the specified timer time elapses integration is automatically reset and restarted Integration repeats until you press Stop However if the integrated value reaches its maximum or minimum displayable value before the specified amount...

Page 84: ...e conditions below is met integration is stopped and the integration time and integrated value are held The scheduled stop time is reached The integration time reaches the maximum integration time 10000 hours The integrated value reaches its maximum or minimum displayable value Real Time Continuous Integration Mode Continuous integration R Continuous Set the date and time when integration starts a...

Page 85: ...w The scheduled integration start time is set to the current time Copy The scheduled integration start time is copied to the scheduled integration stop time When Independent Integration Is Disabled The scheduled times that you specified above apply to every element When Independent Integration Is Enabled Setting You can select the method for setting the scheduled times from the following options E...

Page 86: ...ime Element1 to Element6 Set the integration method to one of the options below Charge Discharge Measure DC watt hours for each sampled data item by polarity Sold Bought Measure AC watt hours for each sampled data item by polarity For information about the equations used in each method see appendix 1 in the getting started guide IM WT1801 03EN Current Mode for Current Integration q Mode Setting Yo...

Page 87: ...hip between the measured integrated D A output value and the voltage see Relationship between Output Items and the D A Output Voltage Click here Setting the Rated Time for Integrated D A Output You can set the hour minute and second within the following range 00000 00 00 to 10000 00 00 This setting is valid in the following integration modes Manual integration mode Real time normal integration mod...

Page 88: ...orm Scale Value The measurement function element number and lower limit of the displayed waveform Trigger level Ground level Waveform label U1 3 000kV U1 3 000kV 0 000s 50 000ms 1602 p p U1 Measurement Mode during Waveform Display When waveforms are displayed the measurement mode indicated in the upper left of the screen is Normal Mode Trg After a trigger occurs measurement takes place at the data...

Page 89: ...nges as described below Single 672 points Dual 336 points Triad 224 points Quad 168 points Hexa 112 points When the screen is split the number of displayed points along the vertical axis of a single window is halved For information about how to assign waveforms to windows see Waveform Mapping Click here Time Axis Time div The time axis is set in Time div time per grid division The time axis can be...

Page 90: ... the number of waveform display data points the number of points displayed on the screen for a single input signal is 1602 p p Compression p p compression is the compression method used to derive waveform display data from waveform sampling data For example if a 2 Hz sine wave is measured at a data update rate of 1 s to display this waveform the WT1800 converts the number of data points from appro...

Page 91: ...easurement range For example if the crest factor is set to CF3 and the voltage measurement range is set to 100 Vrms the display range is set to 300 Vpk 3 100 Vrms with the zero input line at the center The waveform is clipped if this range is exceeded In the same way if the crest factor is set to CF6 and the voltage measurement range is set to 50 Vrms the display range is set to 300 Vpk 6 50 Vrms ...

Page 92: ... source For the EXT CLK connector specifications see section 4 3 in the getting started guide IM WT1801 03EN When Ext Clk is set as the trigger source the trigger level setting is invalid Trigger Slope Slope Slope refers to the signal movement from a low level to a high level rising slope or from a high level to a low level falling slope When the slope is used as one of the trigger conditions it i...

Page 93: ...ger point in the figure below is just for illustration The arrow does not appear on the actual display Trigger point Time To prevent noise related errors the trigger feature has a hysteresis of approximately 1 when the crest factor is set to CF3 For example when the trigger slope is set to a trigger will occur if the input signal level falls approximately 1 below the trigger level and then passes ...

Page 94: ...ertically aligned dots are filled If the number of data points is 1602 or greater the WT1800 determines the P P compression values the maximum and minimum sampled data values in a given interval and displays vertical lines rasters connecting each pair of maximum and minimum P P compression values In the Interpolation Zone Grid Graticule You can set the window grid to one of the following options T...

Page 95: ...the top of the screen and the window number increases for each successively lower window 1 Speed and torque waveforms are available on models with the motor evaluation option 2 Aux1 and Aux2 waveforms are available on models with the auxiliary input option Display Item ITEM Displaying All Waveforms All ON The waveforms of all input signals are displayed Displaying No Waveforms All OFF No waveforms...

Page 96: ...upper and lower display limits of the screen do not correspond to three or six times the measurement range or to 100 when the crest factor is set to CF3 or CF6 respectively You must take the zoom factor into account when setting a waveform s position In the figure below the crest factor is set to CF3 the voltage range is 100 V the zoom factor is 2 and the vertical position has been shifted by 25 T...

Page 97: ...veform display are shown Trend Display Trend You can display the trends of measurement functions Trend Display Example Time at the right edge of the screen amount of time contained in the screen Time at the left edge of the screen fixed at 0 seconds Scale Value The trend number measurement function element and upper limit of the displayed trend Scale Value The trend number measurement function ele...

Page 98: ... trend data is displayed as a line graph with each point separated by 10 s If you set Time div to 1 day div the trend display will be updated once every 1080 s regardless of the data update interval One division 1 div on the trend display is equivalent to 80 rasters For example if you set Time div to 1 day div one raster is 1080 s which is equal to 1 day 80 the trend data update interval is 1080 s...

Page 99: ...t the displayed harmonic order within the following range Total Total value or 0 DC to 500 The orders that can be specified vary depending on the measurement function For details see Harmonic Measurement Function Orders Click here The trends of orders that exceed the maximum measurable order are displayed at the top or bottom of the screen For information about the maximum measurable harmonic orde...

Page 100: ... are used Log Scale if a value is negative its absolute value is displayed with a red bar graph If the analysis window width number of cycles of the fundamental signal that is determined by the fundamental frequency is shorter than the data update interval bar graphs are not displayed Set a longer data update interval For details see Notes about the Numeric Data Display Click here The bar graphs o...

Page 101: ...e options vary depending on the installed elements Element1 Element2 Element3 Element4 Element5 and Element6 Bar Graph Display Scale Setting the Vertical Scale Mode Scale Mode You can set the upper and lower limits of a bar graph window Set the display mode to one of the options below Fixed When the function is U I P S or Q the scaling is logarithmic Log When the function is λ Φ ΦU ΦI Z Rs Xs Rp o...

Page 102: ... 1 0 6016kVA Q2 1 0 2342kvar λ2 1 0 9211 U3 1 101 40 V I3 1 3 4990 A P3 1 0 2128kW S3 1 0 5997kVA Q3 1 0 5067kvar λ3 1 0 3549 Wiring ΣA 3P3W 3V3A PLL Src U1 fPLL1 743 00 Hz ΦU1 U2 57 67 ΦU1 U3 302 78 ΦU1 I1 315 35 ΦU2 I2 22 91 ΦU3 I3 249 22 300 0 V 6 000 A For a 3P4W three phase four wire system U1 1 U2 1 and U3 1 are line voltages I1 1 I2 1 and I3 1 are line currents For a 3P3W three phase three ...

Page 103: ...elect the element or wiring unit to display from the options below The available options vary depending on the installed elements Element1 Element2 Element3 Element4 Element5 Element6 ΣA ΣB and ΣC Setting Vector Zoom Factors U Mag I Mag You can change the sizes of the vectors You can specify separate zoom factors for the fundamental waves U 1 and I 1 When you zoom a vector the value for the size o...

Page 104: ...eric Numeric data Trend Trend Bar Bar graph Vector Vector This item is available on models with the harmonic measurement option or the simultaneous dual harmonic measurement option Split Displays with the Trend Display Trend Trends are displayed in the top half of the screen Select the display to show in the bottom half of the screen from the following options Numeric Numeric data Wave Waveform Ba...

Page 105: ...ement is not performed Waveform Measured by Cursor 1 C1 Trace This item only appears in the waveform and trend displays It does not appear in the bar graph display In the Waveform Display You can select the waveform to measure with cursor 1 from the following options The available options vary depending on the installed elements U1 I1 U2 I2 U3 I3 U4 I4 U5 I5 U6 I6 Speed Torque Aux1 and Aux21 2 1 S...

Page 106: ...ge of the screen to 800 the right edge of the screen Trend display 0 the left edge of the screen to 1601 the right edge of the screen Bar graph display 0 DC to 500 the 500th order Position of Cursor 2 x C2x Position Set the position of cursor 2 x The ranges within which you can set the position are the same as those for cursor 1 C1 Position Click here Linking Cursor Movement Linkage Set Linkage to...

Page 107: ... The date and time of measurement are displayed in this format Year Month Day Hour Minute Second If immeasurable data exists is displayed in the measured value display area ΔY can be measured even when the units of the cursors are different The measured result will not have a unit In the Bar Graph Display Y1 The vertical axis Y axis value of cursor 1 of bar graph 1 Y1x The vertical axis Y axis val...

Page 108: ...lected trend You can set the cursor position relative to the left edge of the screen in points with the left edge itself being 0 points and the right edge being 1601 points You can move through the displayed data one point at a time In the Bar Graph Display Two cursors and x are displayed in each graph Graph1 to Graph3 You can set the cursor positions as orders The bar graph display indicates what...

Page 109: ...ge U current I and power P values for each element and the measured UmeanΣ ImeanΣ Ur meanΣ and Ir meanΣ values for each wiring unit by setting a low cutoff frequency for the HS filter However if you set a low cutoff frequency for the HS filter the response to changes in the measured values becomes slower Display Indications for High Speed Data Capturing High Speed Data Capturing State File Recordi...

Page 110: ...ata capturing continue without stopping Initializing High Speed Data Capturing High speed data capturing is initialized when You switch from normal measurement to high speed data capturing You change one of the following settings A voltage or current measurement mode Whether the HS filter is on or off The HS filter s cutoff frequency Trigger Fundamental measurement conditions such as the measureme...

Page 111: ...ver range is displayed for P OL for over range is displayed for UΣ if even one of the measured voltage values for an input element in a single wiring unit is over range The same is true for IΣ and PΣ UΣ and IΣ are displayed as zero when they are the following percentage of the maximum voltage range or current range out of the input elements assigned to the same wiring unit When the Crest Factor Is...

Page 112: ...ed data capturing Start Stop Number of Data Captures Capture Count The number of captures can be set to infinity or to a value from 1 to 10000000 Viewing and Optimizing the Maximum Capturing Count Optimize Count The WT1800 computes the maximum capturing count for the save destination of the captured data file according to the number of numeric data items specified in Item Settings You can set the ...

Page 113: ...t measurement mode rms mean dc r mean If the voltage and current measurement mode settings differ for elements assigned to the same wiring unit the voltage UΣ and current IΣ of the wiring unit are not measured and are displayed as no data HS Filter HS Filter Turning on the HS high speed filter stabilizes the measured values The HS filter averages the measured values The HS filter is different from...

Page 114: ...level setting Click here External Sync External Sync You can synchronize the WT1800 with another device during measurement by applying an external sync signal to the external start signal I O MEAS START connector OFF The WT1800 does not synchronize with an external start signal but instead captures data every 5 ms ON The WT1800 captures data in sync with an external start signal For the specificat...

Page 115: ...g state to change to Error When you perform consecutive operations in the setup menu When the WT1800 receives consecutive communication commands When you operate the WT1800 over FTP When you save to a USB memory device with a slow write speed When the write speed to the USB memory device that has been specified as the save destination is slow the data update speed exceeds the speed at which the fi...

Page 116: ...V file is created in the root folder of the USB memory device whose ID number is 0 USB 0 An error message appears when USB memory is not connected When the storage destination is a USB memory device USB 0 or USB 1 A CSV file is saved in the same folder as the high speed data capturing data file The WT1800 will not create a CSV file whose size exceeds 2 GB but will instead create a CSV file for 2 G...

Page 117: ...ile name appear in the upper left of the screen While File State Rec is displayed the storage medium is constantly being accessed even though the icon that indicates this is not displayed so do not remove the USB memory device or turn off the power Doing so may damage the storage medium and corrupt its data Stopping High Speed Data Capturing Stop High speed data capturing stops When high speed dat...

Page 118: ...itialization High speed data capturing state HS State Ready Start Ready Stop key or capture count Completion of file recording File recording state File State Ready Rec Trigger Ready Data capturing Trigger wait After a trigger occurs measured data is regularly written to the high speed data capturing data file WTS 16 High Speed Data Capturing ...

Page 119: ...how ON or hide OFF peak over range occurrence information Peak Over Range Occurrence Information Peak Over Status If a peak over range occurs in an input signal even once from the time when high speed data capturing starts until it stops the input signal is displayed in red Display example for when a peak over range has occurred in U1 and I2 When display frames for measured values are displayed di...

Page 120: ...ady The storage mode is real time storage mode integration synchronized storage mode or event synchronized storage mode and the WT1800 is ready to begin storing Cmpl Complete The WT1800 has completed the specified number of storage operations The WT1800 is in real time storage mode and the scheduled storage stop time has passed When storage is reset no storage state is displayed in the upper left ...

Page 121: ...med in integration synchronized storage mode Event Event synchronized storage mode Storage starts after you press STORE START the measured data is updated and a user defined event occurs You can store numeric data each time the measured data is updated until the storage count is reached Single Shot Single shot storage mode Numeric data is stored whenever you press STORE START You can store numeric...

Page 122: ...ode is set to Real Time You can set the year month day hour minute and second of the storage start and stop times Be sure to set the storage stop time to a time after the storage start time You can set the values within the following ranges Year Any four digit Gregorian calendar value Hour Minute Second 00 00 00 to 23 59 59 Now The scheduled storage start time is set to the current time Copy The s...

Page 123: ...the numeric data display format or the displayed items the data is stored according to the numeric data that was displayed at store start Selected Items Selected Items You can select the types of numeric data to store To select which types of numeric data to store click Items Items Items If you set the numeric data items to store to Selected Items you can select which types of numeric data to stor...

Page 124: ...her to automatically create an ASCII format stored data file csv from the stored data file wts and the header file hds that are saved when storage finishes or is reset When the storage destination is the internal RAM disk RAM 0 A CSV file is created in the root folder of the USB memory device whose ID number is 0 USB 0 When the storage destination is a USB memory device USB 0 or USB 1 A CSV file i...

Page 125: ...v Be sure to remove the USB memory after storage has been reset or has completed Cmpl When you turn off the WT1800 power the contents of the internal RAM disk are lost Save the contents of the RAM disk to a USB memory device or network drive before you turn off the WT1800 Please be aware that the number of times that you can write to USB memory is limited Starting Stopping and Resetting Storage ST...

Page 126: ...rage state changes to Stop If integration can be restarted without being reset the storage state changes to Ready Event synchronized storage mode Event Storage continues until the storage count is reached Single shot storage mode Single Shot Storage continues until the storage count is reached After storage is completed the following occurs The STORE STOP key illuminates and Store Cmpl appears in ...

Page 127: ...n STORE RESET key When integration stops before the storage count is reached illustration of operations after integration starts Time STORE START blinking State Ready Start STORE START on Stop Integration reset STORE STOP blinking STORE RESET key Integration start Integration stop If you reset integration after it has been stopped the store state changes to Cmpl Writing to the stored data file wts...

Page 128: ...TORE STOP blinking STORE START key STORE STOP key Storage Operation When the Storage Interval Is Not an Integer Multiple of the Data Update Interval Here we will use the case when the data update interval is 5 s and the storage interval is 7 s as an example How storage is performed varies as indicated below depending on the storage mode When the Storage Mode Is Not Set to Integ Sync Storage is per...

Page 129: ... interval is 00 00 00 or when Storage Mode is set to Event The storage operation stops but integration does not When the storage mode is set to Single Shot The held display values are stored Even during integration the held display values are stored In All Other Cases The held display values are stored During integration the values being measured are stored Media access indication icon only illumi...

Page 130: ...EG format jpg Binary format wts hds PC Microsoft Excel WTViewer Online1 Offline2 Online1 Offline2 ASCII format csv Numeric data Numeric data Waveform display data Waveform display data Screen image data BMP format bmp PNG format png JPEG format jpg Binary format wtw Waveform display data File Reader Storage Media The WT1800 can access the following three types of storage media for saving and loadi...

Page 131: ...bout the file save conditions see File Save Conditions Click here Saving Waveform Display Data Save Wave You can save the waveform data that the WT1800 has measured to a file in ASCII format csv The waveform displayed on the screen is saved For information about the file save conditions see File Save Conditions Click here The waveform display data that the WT1800 saves is not the sampled waveform ...

Page 132: ... 16 value display would appear when you pressed NUMERIC then the data for the measurement functions on the page of the 16 value display that would appear is saved Selected Items Selected Items You can select the types of numeric data to save Items Items If you selected Selected Items select which numeric data to save Element Element To select an element or wiring unit that you want to store the da...

Page 133: ...incremented sequence number 000 to 999 as its name and the data continues to be saved in the new folder File Name File Name You can set the common file name that is used when the auto naming feature is turned off or when the auto naming feature is set to Numbering The maximum number of characters that you can use for file names and folder names is 32 characters The following restrictions apply The...

Page 134: ...ing or saving is cancelled measurement resumes To save data when the data update interval is 20 s enable the hold feature perform a single shot measurement and then save the data after the data update for the single shot measurement has completed Because the header files saved by the WT1800 use a format that is common to YOKOGAWA measurement devices they contain some data that is not used by the W...

Page 135: ...ecting the Type of File to List File Filter You can limit the type of files that appear in the list by selecting an extension Changing the Storage Medium Change Drive You can select the storage medium that you want to access The WT1800 displays the storage media as follows RAM 0 The internal RAM disk of the WT1800 USB 0 The first USB memory device connected to a WT1800 USB port USB 1 The second US...

Page 136: ...ll Files ALL Reset All of the selected files and folders are deselected Jumping to a Specified File or Folder Jump To You can make the cursor jump to a file or folder at a specified numeric position in the file list The numeric position at the top of the file list is 0 Range 0 to 999 Other Operations More You can select from the following operations Sort To Sort the file list Display Type Select t...

Page 137: ...r mode PNG The extension is PNG The file size is approximately 25 KB for black and white mode and approximately 100 KB for color mode JPEG The extension is JPG The file size is approximately 200 KB for color mode The file sizes listed here are for reference Actual file sizes will vary depending on the image that is saved Screen Image Colors Color You can select the color format to save to from the...

Page 138: ...ts are printed in the order that they are displayed When numeric values are displayed in the single or dual harmonics list In addition to the data described above the data of harmonics that are not displayed on the screen is printed up to the maximum measurable order Max Order When numeric values are displayed in the All Items or Custom display Printing cannot be performed If you attempt to print ...

Page 139: ...starts and stops in synch with the scheduled printing start and stop times Data is printed at each print interval Integ Sync Integration Synchronization Print Mode Printing starts and stops in synch with the starting and stopping of integration Data is printed at each print interval Event Event Synchronization Print Mode When you enable automatic printing printing is executed when the measurement ...

Page 140: ...py The scheduled printing start time is copied into the scheduled printing stop time You can set the day for the scheduled start or stop time in February to a value as high as the 31st day If you do so an error message will appear when you enable automatic printing Reset the scheduled start and stop times The WT1800 recognizes leap years when it executes automatic printing Trigger Event Trigger Ev...

Page 141: ... Tp Real Time Print Mode When the scheduled start time is before Auto Print ON Time Start time Auto Print ON PRINT key on Auto Print OFF or the ending time Printing PRINT key off Tp Print interval Data is printed if Print at Start is set to ON Tp Tp Tp Tp When the scheduled start time is after Auto Print ON Time Start time PRINT key blinking Auto Print ON PRINT key on Auto Print OFF or the ending ...

Page 142: ...INT key off Tp Print interval Data is printed if Print at Start is set to ON Tp Tp Integration Timer and Print Interval in Continuous Integration Mode and Real Time Continuous Integration Mode Printing is executed whenever the integration timer time elapses Time Integration start Integration time up integration restart PRINT key on Forced integration stop Printing Tp Print interval Data is printed...

Page 143: ...int is longer than the data update interval Time Event occurrence Auto Print ON PRINT key on Printing PRINT key off T Event occurrence F No event occurrence Td Data update interval Tpe Time it takes to print Td Td Td Td Td Td Td Td Auto Print OFF T T T F F T T T Tpe Tpe Tpe Printing PRINT Prints the screen image data or numeric data list Using an External Signal to Control Printing Option On model...

Page 144: ...WT1800 from a PC on the same network and retrieve setup data numeric data waveform display data and screen image data Click here Network Drive Net Drive You can save the WT1800 s setup data numeric data waveform display data and screen image data to a network drive You can also load the setup data from a network drive into the WT1800 Click here SNTP The WT1800 clock can be set using SNTP When the ...

Page 145: ...st by name instead of by IP address Set the domain name and the DNS server address 0 0 0 0 by default For details consult your network administrator DNS Servers DNS Server1 DNS Server2 You can specify up to two DNS server addresses primary and secondary If querying fails with the primary DNS server the secondary DNS server is automatically used to find the mapping of the host name and domain name ...

Page 146: ...to access the WT1800 from a PC Number of characters Up to 32 Usable characters All ASCII characters that are displayed on the keyboard Timeout Time Out If an FTP connection cannot be established between the WT1800 and the PC within the amount of time specified here the WT1800 aborts the connection process You can set the timeout time to a value between 1 and 3600 To apply the settings that you spe...

Page 147: ...yed on the keyboard Password Password Specify the password that corresponds to the login name Number of characters Up to 32 Usable characters All ASCII characters that are displayed on the keyboard Passive Mode Passive Turn passive FTP on or off In passive mode the FTP client sets the port number for data transfer Enable passive mode when you have set an external FTP server as a network drive or w...

Page 148: ...hronized to the SNTP server clock Automatic Adjustment Adjust at Power ON You can configure the WT1800 so that its clock is automatically synchronized to the SNTP server clock when the WT1800 is turned on when it is connected to the network Setting the Time Difference from Greenwich Mean Time Time Difference From GMT This is the same as the Setting the Time Difference from Greenwich Mean Time Time...

Page 149: ...ting a PC to the WT1800 to control it Click here System Configuration System Config You can set the date and time time synchronization the menu and message languages the LCD intensity whether the backlight is on or off the USB keyboard language and USB communication and you can format storage media Click here Ethernet Communication Network You can configure TCP IP FTP server network drive and SNTP...

Page 150: ...ed Version Suffix Code New Features 2 01 or later HS High Speed Data Capturing features Chinese and German have been added to the menu language and message language Initializing the Settings Initialize Settings You can reset the WT1800 settings to their factory default values This feature is useful when you want to cancel all of the settings that you have entered or when you want to redo measureme...

Page 151: ...T1800 or with other devices through GP IB do not change the address Notes about Connections Several cables can be used to connect multiple devices However no more than 15 devices including the controller can be connected on a single bus When connecting multiple devices you must assign a unique address to each device Use cables that are 2 m or shorter in length to connect devices Keep the total len...

Page 152: ...he timeout time to infinity or a value between 1 and 3600 You must set TCP IP parameters to connect the WT1800 to an Ethernet network Click here Notes about Connections To connect the WT1800 to a PC be sure to use straight cables through a hub Correct operation is not guaranteed for a one to one connection using a crossover cable Use one of the following types of network cables that support the da...

Page 153: ...eenwich Mean Time Time Difference From GMT This setting appears when the method for setting the date and time is set to SNTP Set the time difference between the region where you are using the WT1800 and Greenwich Mean Time to a value within the following range 12 hours 00 minutes to 13 hours 00 minutes For example Japan standard time is ahead of GMT by 9 hours In this case set Hour to 9 and Minute...

Page 154: ...he menu language will also be set to Chinese Adjusting the LCD LCD You can turn off the LCD and adjust its brightness Turning Off the LCD LCD Turn OFF You can turn off the LCD When the LCD is off you can turn it back on by pressing a key Automatically Turning Off the LCD Auto OFF The LCD turns off automatically when there are no key operations for a given time period The LCD turns back on when you...

Page 155: ...Resolution You can choose to display four digits or five digits of the numeric data The number of displayed digits for integration measurement functions is fixed at six Frequency Display When the Frequency Measurement Is Less Than Lower Limit Freq Display at Frequency Low When the frequency of the input signal is lower than the frequency that the WT1800 can measure you can choose to display the fr...

Page 156: ...V Order Order option When you select a function that has harmonic data you can set the displayed harmonic order within the following range Total Total value or 0 DC to 500 The orders that can be specified vary depending on the measurement function For details see Harmonic Measurement Function Orders Click here The outputs of orders that exceed the maximum measurable order are 0 V For information a...

Page 157: ...e scaled measured value is the same as the scaled rated value measurement range scaling factor For Σ functions the WT1800 produces 100 output 5 V when the measured value is equivalent to the value that is measured when all of the elements in the group are at their rated values When the elements have different scaling factors the WT1800 produces 100 output 5 V when the scaled measured values are th...

Page 158: ...f torque per 1 V of input voltage the output is 5 V when the torque is 10 N m The output for an analog rotating speed signal is 5 V when the rotating speed reaches the value of the input range the revolution scaling factor the input signal slope this is the rated value 1 For example when the input range is 10 V if the scaling factor is set to 100 rpm per 1 V of input voltage the output is 5 V when...

Page 159: ... is displayed the key is operating properly If the indicators on the front panel turn on and off in order when you press the left and right cursor keys they are operating properly To exit the key test press ESC twice Keyboard Test Soft Key This test appears when you set Test Item to Key Board You can test whether the keyboard displayed on the screen is functioning properly If the characters that y...

Page 160: ...nsation There is a feature that automatically performs zero level compensation during integration integration auto calibration Click here NULL Feature NULL SET You can use the NULL feature to subtract the DC offset while a measurement cable or external sensor is connected Items to Configure NULL Settings for Target Element All Each time you press NULL you can enable or disable the NULL feature for...

Page 161: ...aved NULL value discussed above is used to correct the measurement function values OFF Even if you press NULL the NULL feature is not enabled Measurement function values are produced with no NULL correction The held NULL value is cleared under the following circumstances Operations that cause the NULL values of all inputs to be cleared Turning on the power the NULL values are not backed up when yo...

Page 162: ... enabled or disabled while the display is held the NULL indicator will illuminate or turn off but the held data will not be affected Also the NULL indicator will be highlighted The DC values that the NULL value is based on when the NULL feature is ON are held but the upper limit of the NULL value is 10 of the range when the crest factor is set to CF3 The upper limit of the NULL value is 20 of the ...

Page 163: ...ale 12 2 bar graph display windows number of 12 1 bar graph number 12 2 C Page C1 Position 15 2 C1 Trace 15 1 C2x Position 15 2 C2x Trace 15 1 CAL 23 1 calculation 4 4 5 2 capture control settings 16 5 capture count 16 4 Clear Trend Exec 11 2 color 19 1 22 6 Column No 7 7 16 11 Column Num 7 7 16 11 column number 7 7 16 11 columns 7 7 columns number of 7 7 16 11 column settings 7 7 comment 18 5 con...

Page 164: ...color 7 11 font size 7 11 FORM high speed data capturing 16 4 FORM numeric data 7 1 FORM trend 11 2 FORM bar graph 12 1 FORM waveform 10 2 FORM vector 13 2 format 10 2 12 1 FREQ FILTER 2 19 FREQ MEASURE 8 11 frequency filter 2 19 frequency measurement 8 11 frequency measurement source 4 7 FTP server 21 3 FU FI η 7 5 G Page GP IB 22 3 graticule 10 7 Greenwich Mean Time 21 5 22 5 grid 10 7 grid inte...

Page 165: ... offset value auxiliary input 5 2 offset value motor evaluation 4 3 optimization 16 4 17 2 optimize count 16 4 17 2 order 1 4 other displays 11 1 OTHERS 11 1 overview 22 2 P Page p p compression 10 3 PAGE DOWN 7 3 PAGE END 7 3 PAGE TOP 7 3 PAGE UP 7 3 paper feeding 20 3 Pc formula 8 9 peak over range jump 2 16 peak over status 16 11 phase 8 10 phase difference 8 10 PLL source 3 1 pole 4 7 power co...

Page 166: ...17 7 store set 17 1 store start 17 6 store stop 17 7 string 7 11 synchronization source motor evaluation 4 5 synchronized measurement 8 10 synchronous speed 4 7 sync measure 8 10 Sync Source 4 5 sync source 2 18 sync speed 4 7 system config 22 5 system overview 22 2 system settings 22 5 T Page TCP IP 21 2 test items 22 11 Thd formula 3 3 time div 10 2 11 2 time axis 10 2 11 2 time difference from ...

Page 167: ...method for each polarity 9 11 watt hours 9 1 waveform display 10 1 waveform display data saving 18 2 waveform display windows number of 10 2 waveform labels 10 7 waveform mapping 10 8 waveforms methods for assigning to screens 11 2 waveform sampling data 10 3 wave label 10 7 wave mapping 10 8 Wiring 2 1 wiring 2 1 wiring system 1 6 2 1 wiring system combination 2 1 wiring unit 1 6 2 1 WP q TIME 7 ...

Reviews:

No comments

Related manuals for WT1800

TUNICS T100S-HP

Brand: Yenista Optics Pages: 66

Brand: Larson Davis Pages: 193

Brand: Facom Pages: 116

Brand: PASCO Pages: 3

Brand: PASCO Pages: 2

Brand: NanoPhotometer Pages: 133

Brand: A&D Pages: 39

Brand: Pasco Scientific Pages: 11

Brand: H-Star Pages: 36

Brand: PITSID Pages: 22

Brand: Swan Analytical Instruments Pages: 102

Microlog GX Series

Brand: SKF Pages: 342

Brand: CAS Corporation Pages: 20

Brand: Sagola Pages: 16

Brand: KEM Pages: 49

CR-2010 PRO Series

Brand: G-Tek Pages: 48

Brand: Keysight Pages: 26

MJK MagFlux Series

Brand: Xylem Pages: 179

Brands by name

0 1 2 3 4 5 6 7 8 9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Popular brands

Load more brands