1xEV-DO Measurements
R&S
®
CMW-KM8xx/-KS8xx
242
User Manual 1173.9511.02 ─ 12
3.2.6.2
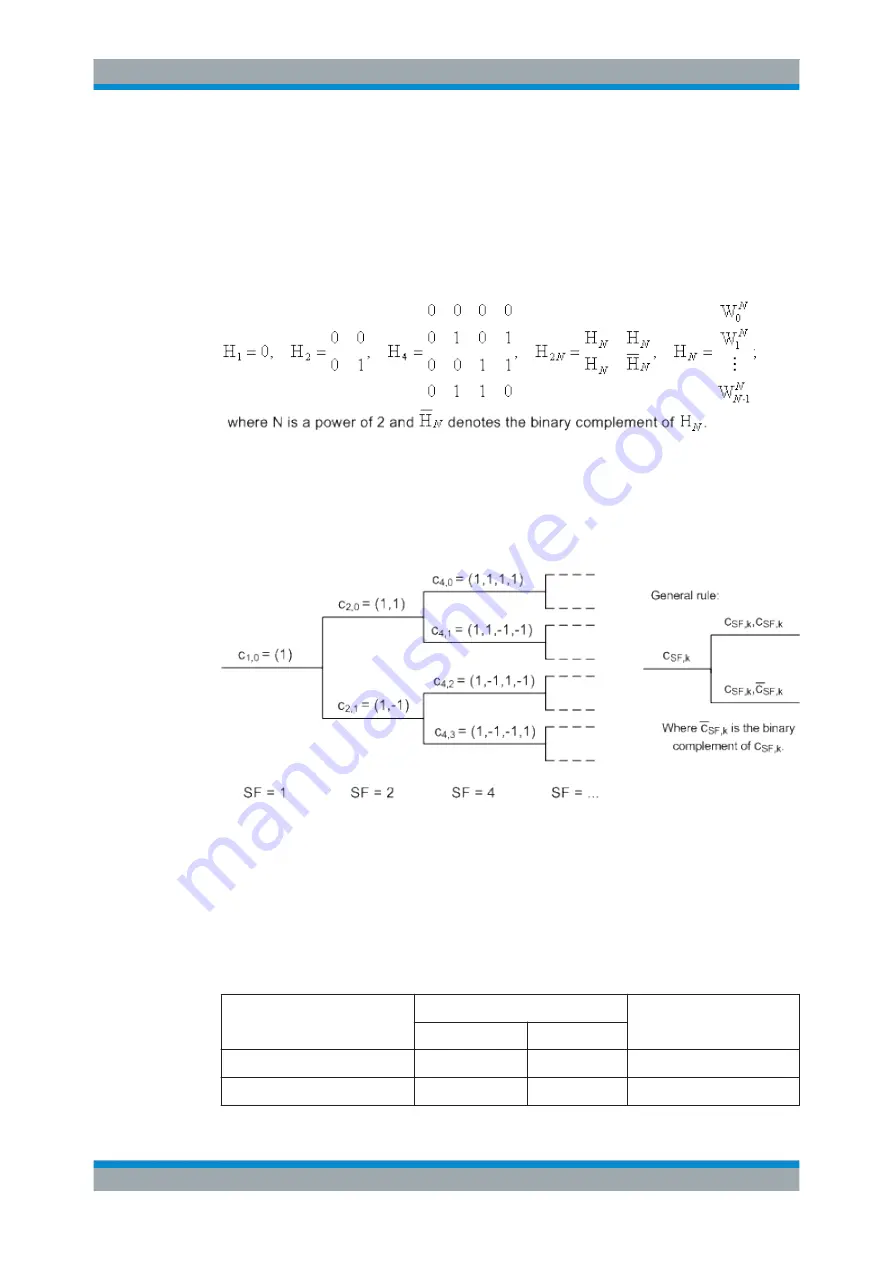
Channelization
1xEV-DO channels are spread using orthogonal Walsh functions W
n
N
defined in terms
of the order N of the function and the index n ranging from 0 to –1. This index is also
called channelization code number. The Walsh functions are serially constructed from
a N x N Hadamard matrix, generated by means of the following recursive procedure
defined in 3GPP2 C.S0002:
For the spreading operation the binary symbols of the Walsh function are mapped as
follows: "0" is mapped to +1 and "1" is mapped to "-1".
Orthogonal Variable Spreading Factor (OVSF) codes provide an alternative scheme of
generating codes that preserve orthogonality between channels. They are derived from
a hierarchical tree:
The OVSF spreading factor SF corresponds to the Walsh function order N. For a given
spreading factor SF, Walsh codes and OVSF codes can be derived from each other
via the binary representation of the channelization code numbers. The Walsh code with
code number n is equal to the OVSF code with code number m, where m has the
inverse binary representation of n (n is converted into m by reversing the order of bits
in the binary representation of n). For numbers with symmetrical binary representation
(e.g. 00 or 1001), the Walsh code and OVSF code numbers are equal.
Example for SF=4 and N=4:
Hadamard (Walsh codes)
after mapping to +1/-1
Code number
Bit reverse (OVSF codes)
decimal
binary
1 1 1 1
0
00
1 1 1 1
1 -1 1 -1
1
01
1 1 -1 -1
General Description
深圳德标仪器
135-1095-0799






























